SOLUTION: Assume there are 5 braille dots (raised and flat) on a given surface. How many letters are possible if at least 1 dot is raised?

As I understand the question, it is not about real letters for blind persons.


It is about abstract "letters", that are defined as different combinations of raised dots on a given surface.


The number of different combinations of raised dots is equal to the number of all subsets of the set of 5 elements.


It is well known fact that the number of all subsets of any finite set of N elements is  , incliding

the empty subset and the proper subset.


Since the empty subset is excluded by the condition,  we have for N= 5 given braille dots 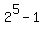  = 32-1 = 31  possible non-empty subsets,

and, hence, 31 possible "abstract" letters.