Question 1117842: How many different non-congruent isosceles triangles can be formed by connecting three of the dots in a 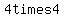 square array of dots like the one shown below?
. . . .
. . . .
. . . .
. . . .
Two triangles are congruent if they have the same traced outline, possibly up to rotating and flipping. This is equivalent to having the same set of 3 side lengths.
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
The possible side lengths are those which can be obtained by going 0, 1, 2, or 3 units both horizontally and vertically.
(0,0) --> 0 this one obviously doesn't count
(0,1) --> 1
(0,2) --> 2
(0,3) --> 3
(1,1) --> sqrt(2)
(1,2) --> sqrt(5)
(1,3) --> sqrt(10)
(2,2) --> sqrt(8)
(2,3) --> sqrt(13)
(3,3) --> sqrt(18)
It should be clear that there will be no isosceles triangles in this array of dots that have all integer side lengths. So look at each irrational side length and see what isosceles triangles you can make with each one.
(1) With a single side of length sqrt(2), there are three triangles. The congruent sides have lengths 2, sqrt(5), or sqrt(13).
(2) With two sides of length sqrt(2), there is one triangle, with third side length 2.
(3) Experimentation should show that there are no isosceles triangles with a single side of length sqrt(5). With two sides of length sqrt(5), there are two different isosceles triangles -- one with side length 2 and one with side length sqrt(10).
(4) With a single side of length sqrt(8), there are again two isosceles triangles -- one with side length 2 and one with side length sqrt(10).
(5) Experimentation should show that there are no isosceles triangles with a single side of length sqrt(13).
(6) And with a side length of sqrt(18) there is only one isosceles triangle -- with the other two side length 3.
So there are 9 kinds of isosceles triangles that can be formed:
(1) sqrt(2), 1, 1
(2) sqrt(2), sqrt(5), sqrt(5)
(3) sqrt(2), sqrt(13), sqrt(13)
(4) sqrt(2), sqrt(2), 2
(5) sqrt(5), sqrt(5), 2
(6) sqrt(5), sqrt(5), sqrt(10)
(7) sqrt(8), 2, 2
(8) sqrt(8), sqrt(10), sqrt(10)
(9) sqrt(18), 3, 3
|
|
|
