Question 1117810: What is the value of the constant term of 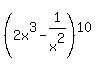
Found 3 solutions by solver91311, greenestamps, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by greenestamps(13218)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To get a constant term, you need to take the term with x^3 4 times and the term with (1/x^2) 6 times:
 which is a constant. which is a constant.
Taking the (2x^3) term 4 times out of 10 and the (-1/x^2) term 6 times gives you a coefficient (and therefore a constant term) of

Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Writing by other tutors leaves you without a guidance on how to get this magic/miracle value k = 6 (the "seventh term").
Therefore, below I placed the full solution with detailed explanations of all auxiliary moments.
The binomial expansion is this formula
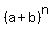 = =  + + 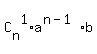 + + 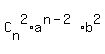 + + 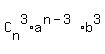 + . . . + + . . . + 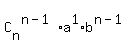 + + 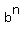 In our case, n = 10, a =
In our case, n = 10, a = 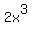 , b = , b = 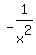 , therefore, the binomial expansion in out case is , therefore, the binomial expansion in out case is
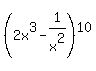 = = 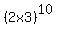 + + 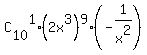 + + 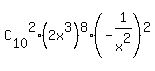 + + 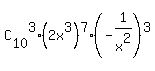 + . . . + + . . . + 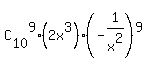 + + 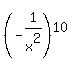 .
The common term is .
The common term is 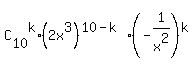 .
This common term is the constant term at 3*(10-k) - 2k = 0, i.e. 30 - 3k - 2k =0, or 30 = 5k ====> k = .
This common term is the constant term at 3*(10-k) - 2k = 0, i.e. 30 - 3k - 2k =0, or 30 = 5k ====> k =  = 6 (the seventh term).
Then the coefficient at this term is = 6 (the seventh term).
Then the coefficient at this term is 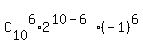 = = 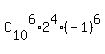 = = 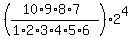 = 3360. = 3360.
The problems like this one are very standard, and you can often meet them on exams or on tests.
Therefore, it is beneficiary for you to have and to know this standard and full solution.
* * * Memorize it as a mantra ! * * *
===================
To see other similar solved problems, look into the lessons
- Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion, Problem 2
- Solved problems on binomial coefficients, Problems 1 and 2
in this site.
|
|
|