Question 1116460: 5. Verify the identity. Justify your steps.
a) nC0 = 1
b) n+1Cr = nCr + nCr-1
c) nC1 = nP1
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note about notation I will use:
1. nCr = C(n,r) = 
2. nPr = P(n,r) = 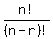
I will do b) which is the hardest part. Furthermore, I will do it algebraically only (it doesn't provide any great insight, but there are good websites that use arrangements of subsets of n and n+1 elements and use a logical argument to show the equality holds):
Left Hand Side (LHS): C(n+1,r) = 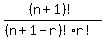
RHS: C(n,r) + C(n,r-1) = 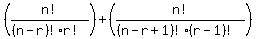
The RHS can be re-written:
= 
factor out 
= 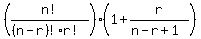
put 2nd factor over common denominator
= 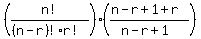
simplify 2nd factor
= 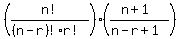
combine loose factors into factorials, e.g. (n+1)*n! = (n+1)!, etc.
=  = LHS (DONE) = LHS (DONE)
To do (a), remember 0! = 1 then use equation 1.
To do (c), plug into 1. and 2. and compare.
==================================
Intuitive argument for (b):
Start with a set S of n+1 elements: S = { X1, X2, X3, …, Xn, Xn+1 }
Obviously you can choose r elements from this set in C(n+1, r) ways. That's the LHS.
Now label one element of S with a *, it doesn't matter which one.
In choosing r elements from S, there are two possibilities: (1) exclude element * or (2) include element *.
If it is excluded, that means you are choosing r elements from the remaining n, and that can be done in C(n,r) ways.
Case (2). If element * is included, you are choosing element * (only 1 way to do this) and r-1 elements from the remaining n elements: this can be done in C(n,r-1) ways.
We must add these two mutually exclusive possibilities: C(n,r) + C(n,r-1). That's the RHS and it is equal to the LHS.
|
|
|