Question 1116072: Ten students are to sit for an examination. Four students are doing mathematics and the other 6 different subjects. In how many ways can they be seated in a row if students doing mathematics are not to sit together?
The solution for this is 6!x7x6x5x4 but I got taught a different method and it did not work. I was taught to group all the maths people together so that there are now 7 groups. I then did 10!-7! to get the number of ways maths people not sitting together. I am really struggling with this questions and I would really appreciate it if you could post the solution and explain how you got to the answer (which is 604800). Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE WAY THE SOLUTION WAS CALCULATED:
I have to agree with the  solution. solution.
 is the number of ways that you can arrange is the number of ways that you can arrange  non-math students in a row. non-math students in a row.
Get those students in the examination room, and let them pick spots in the row of chairs.
Ask each of them to leave empty seats in between them.
Remove the chairs that have no one sitting next to them.
You have now  empty spots empty spots
where you can place the math students
in a row of 6+7=13 seats.
As each math student walks in, let them choose among the 7 empty seats.
There are  different ways they can choose. different ways they can choose.
The first math student has 7 choices;
the second one has 6;
the third one has 5,
and the last one has 4 choices.
WHY 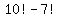 DOES NOT WORK: DOES NOT WORK:
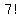 is the number of ways you can get 7 groups in a row is the number of ways you can get 7 groups in a row
so that all the members of each group are together.
As a consequence, 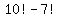 is the number of ways to place the 10 students to avoid having all 4 math students together, but not preventing cluster of 3 math students seating together, or pairs of math students seating together. is the number of ways to place the 10 students to avoid having all 4 math students together, but not preventing cluster of 3 math students seating together, or pairs of math students seating together.
ANOTHER WAY:
Out of 10 seats in a row, numbered 1 through10,
there are only 35 ways to pick 4 non-contiguous seats for the math students:
 . .
For each of those choices, you can have
 different seating orderings for the math students, and different seating orderings for the math students, and
 different seating orderings for the non-math students. different seating orderings for the non-math students.
That multiplies to
 different seating arrangements. different seating arrangements.
|
|
|