Question 1114944: A manager wants to assign 20 workers to four distinct construction jobs. These jobs require 6, 4, 3, and 7 workers respectively. In how many different ways can the manager assign the workers?
Found 2 solutions by math_helper, greenestamps:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think it would be 20C6 * 14C4 * 10C3 * 7C7 = 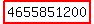 ways. ways.
—
It seems arbitrary to assign the group of 6 workers first, but this result is independent of which group you assign first. Even if you group, say, the 7 workers first for their job, the result is the same:
20C7 * 13C6 * 7C4 * 3C3 = 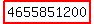 ways. ways.
—
Of course, more complex assignments are possible (assign job 1 to a person from group of 6, assign job 2 to a person from the group of 3, etc.), but the number of possible ways should still be the same.
Answer by greenestamps(13198)   (Show Source): (Show Source):
|
|
|