How many different words can be made out of the letters of the word ALLAHABAD?
The answer would be 9! if the A's and also the L's were distinguishable.
But since the 4 A's are indistinguishable, we must divide by 4!. Also
since the 2 L's are indistinguishable, we must also divide by 2!.
Answer = 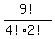

In how many of these with the vowels occupy the even places?
They are all of the form _A_A_A_A_ where the 5 consonants B,H,D,L,L
fill the blanks.
This number is the same as the number of distinguishable arrangements
of consonants BHLLD, which is 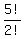

 Edwin
Edwin