SOLUTION: In a basketball game competition, there are many teams and each team plays with each other once. Find the total number of matches played if there are 3 teams?

If "n" teams play each with other and only once, then the total number of matches is .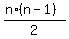


It is easy to understand:  each team plays with (n-1) others.

So, it looks like there are n(n-1) matches in all.


But counting in this way, we count each match twice, for one and for other team.


Therefore, we must divide n*(n-1) by 2 to get the correct answer.  


For 3 teams the answer is  = 3,

and the list of matches (combinations of the team A, B and C) is THIS:


(A,B), (A,C) and (B,C).

    - the number of handshakes between "n" people;

    - the number of diagonals of n-sided polygon;

    - the number of straight lines in a plane, connecting "n" given points
          placed in a way that NO 3 points lie in one straight line.