.
A) In how many ways can the two-person team be formed?
In 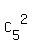 =
=  = 10 ways.
B) In how many ways can the three-person team be formed?
In
= 10 ways.
B) In how many ways can the three-person team be formed?
In 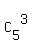 =
=  = 10 ways.
C) In how many ways can the company organize the available people into two or three person teams?
If you select 2 persons for a 2-persons team, then the remaining 3 automatically form the team of a 3-persons team.
Therefore, the answer in this case is the same "10 ways", as in cases A) and B).
By the way, due to THE SAME REASON, the answers for cases A) and B) coincide.
= 10 ways.
C) In how many ways can the company organize the available people into two or three person teams?
If you select 2 persons for a 2-persons team, then the remaining 3 automatically form the team of a 3-persons team.
Therefore, the answer in this case is the same "10 ways", as in cases A) and B).
By the way, due to THE SAME REASON, the answers for cases A) and B) coincide.