Question 1098954: Suppose five integers are chosen successively at random between 0 and 15, inclusive. Find the probability that:
(Round your answer to four decimal places if necessary.)
a. not more than 2 are the same?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are 16 integers from 0 to 15, inclusive.
There are three cases:
Case 1: The sequence of five choices of integers contains
no integers which are the same.
16 ways to choose the 1st integer.
15 ways to choose the 2nd integer.
14 ways to choose the 3rd integer.
13 ways to choose the 4th integer.
12 ways to choose the 5th integer.
That's (16)(15)(14)(13)(12) = 16P5 = 524160 for case 1
Case 2: exactly 1 pair of the integers are alike, and
the other three integers are all different, and different
from the one pair of like integers.
First we choose the 5 integers and then we order them as
choice 1, choice 2,..., choice 5
We can choose the integer for the one like pair in 16 ways.
We choose the other 3 integers in 15C3 = 455 ways
That's (16)(455) = 7280
Now that we have chosen the set of integers to be chosen, we
now find the number of ways in which each set can be arranged
in a sequence.
Each of those 7280 combinations can be arranged in the
same number of ways as the number of distinguishable
permutations of the word THERE, which has 2
indistinguishable E's. which is 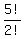 or 60 ways.
So that's (7280)(60) = 436800 ways for case 2.
Case 3: exactly 2 pairs of like integers, both pairs
different from each other, and the 1 remaining single
integer different from either of the two pairs of like
integers.
As in case 2, we first choose the integers and then we
order them.
We can choose the two integers for the two pairs in
16C2 = 120 ways. We can then choose the remaining single
integer in 14 ways. That's (120)(14) = 1680 ways to
choose the integers for the two pairs and the remaining
integer.
Now that we have chosen the set of integers to be chosen, we
now find the number of ways in which each set can be arranged
in a sequence.
Each of those 1680 combinations of integers can be arranged
in the same number of ways as the number of distinguishable
permutations of the word LEVEL, which has 2 indistinguishable
E's and 2 indistinguishable L's. which is or 60 ways.
So that's (7280)(60) = 436800 ways for case 2.
Case 3: exactly 2 pairs of like integers, both pairs
different from each other, and the 1 remaining single
integer different from either of the two pairs of like
integers.
As in case 2, we first choose the integers and then we
order them.
We can choose the two integers for the two pairs in
16C2 = 120 ways. We can then choose the remaining single
integer in 14 ways. That's (120)(14) = 1680 ways to
choose the integers for the two pairs and the remaining
integer.
Now that we have chosen the set of integers to be chosen, we
now find the number of ways in which each set can be arranged
in a sequence.
Each of those 1680 combinations of integers can be arranged
in the same number of ways as the number of distinguishable
permutations of the word LEVEL, which has 2 indistinguishable
E's and 2 indistinguishable L's. which is
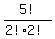 or 30 ways.
So that's (1680)(30) = 50400 ways for case 2.
Grand total for all three cases: 524160+436800+50400 = 1011360
So 1011360 is the numerator of the desired probability.
The denominator of the desired probability is the number of
possible sequences of choices:
16 ways to choose the 1st integer.
16 ways to choose the 2nd integer.
16 ways to choose the 3rd integer.
16 ways to choose the 4th integer.
16 ways to choose the 5th integer.
So the denominator of the desired probability is 165
or 1048576
So the desired probability is or 30 ways.
So that's (1680)(30) = 50400 ways for case 2.
Grand total for all three cases: 524160+436800+50400 = 1011360
So 1011360 is the numerator of the desired probability.
The denominator of the desired probability is the number of
possible sequences of choices:
16 ways to choose the 1st integer.
16 ways to choose the 2nd integer.
16 ways to choose the 3rd integer.
16 ways to choose the 4th integer.
16 ways to choose the 5th integer.
So the denominator of the desired probability is 165
or 1048576
So the desired probability is 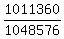 which reduces
to which reduces
to 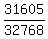 , rounded to 4 decimal places is 0.9645
Edwin , rounded to 4 decimal places is 0.9645
Edwin
|
|
|