Question 1098700: How many distinguishable course codes can be obtained by rearranging MAA2312? Note that the 3 letters must come first and then the 4 numbers.
Found 2 solutions by ikleyn, math_helper:
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Regarding first three letters, there are 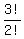 = 3 distinguishable words/arrangements.
Regarding last four digits, there are = 3 distinguishable words/arrangements.
Regarding last four digits, there are 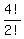 = 12 distinguishable arrangements.
In all, 3*12 = 36 distinguishable course codes can be obtained. = 12 distinguishable arrangements.
In all, 3*12 = 36 distinguishable course codes can be obtained.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ans:  different course codes different course codes
—
Workout:
There are 3 unique arrangements of MAA (to see this, assume you had  , ,  , and , and 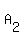 , there would be 3! = 6 ways to arrange those, but we need to divide by 2!, because , there would be 3! = 6 ways to arrange those, but we need to divide by 2!, because 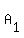 and and 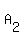 are really just "A" and therefore not distinguishable, so we need to divide that 6 by the number of arrangements of are really just "A" and therefore not distinguishable, so we need to divide that 6 by the number of arrangements of 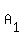 and and 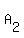 : 6/2 = 3) : 6/2 = 3)
-
There are 12 unique arrangements of 2,3,1,2 (4!/2! = 24/2 = 12)
-
3*12 = 36
|
|
|