Question 1084381: If a(k) = 5+5^2+5^3+5^4+...+5^k , for which of the following values of k will a(k) be divisible by 10?
F) 37 G) 51 H) 75 J) 88 K) 91
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
THE FAST WAY TO THE ANSWER:
All the terms are odd numbers, and you can never get an even sum (such as any multie of 10) by adding an odd number of terms.
That eliminates all the choices, except the one above.
THE SHOW-YOUR-WORK EXPLANATION:
That is a geometric series, the sum of consecutive terms of a geometric sequence (or geometric progression, depending on where you study math).
The sum in this problem is the sum of the first k terms of a geometric sequemce
starting with first term  , and with a common ratio of , and with a common ratio of  . .
That is  . .
For that to be a multiple of 10, we need 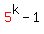
to be a multiple of 8.
There is a way to look at numbers grouping them according to divisibity by a fixed number of interest to us.
All numbers divisible by 8 would be said to be congruent with zero modulo 8,
because they are 0 more than a multiple of 8.
For positive numbers, we would say they are congruent with the remainder we get when we divide them by 8.
(That is modular arithmetic, where you add and multiply lime a clock,
except for modulo 8 there would only be numbers 1 through 8 on the clock)
As we go from one power of 5 to the next,
 is congruent with 1 modulo 8; is congruent with 1 modulo 8;
 is congruent with is congruent with  ; ;
 is congruent with is congruent with  , ,
and also congruent with  } , because } , because  is congruent with is congruent with  . .
 is congruent with is congruent with  ; ;
 is congruent with is congruent with  , ,
 is congruent with is congruent with  , ,
and so on.
So, 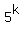 is congruent with 1 modo 8 for all even k numbers, is congruent with 1 modo 8 for all even k numbers,
and it is congruent with 5 modulo 8 for all odd k numbers.
That means that 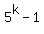 is congruent with is congruent with  modulo 8, modulo 8,
so it is a multiple of 8, making the sum a multiple of 10.
|
|
|