Question 1076286: I am developing a game where a result of 6 or more equals a Hit. I am stuck trying to find a formula for throwing multiple dice and scoring Hits on a sum of 6 or more e.g. for 1 die the answer is 1, for 2 dice it is 26 (?). Add a third dice or more and I am lost. Can anyone help please? Neil
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Yes, one die has one outcome.
Yes, two dice has 26 outcomes greater than or equal to 6.
Moving forward look at the 10 outcomes that are less than 6.
(1,1)=2
(1,2)=3
(1,3)=4
(1,4)=5
(2,1)=3
(2,2)=4
(2,3)=5
(3,1)=4
(3,2)=5
(4,1)=5
Now when you add the third dice you'll have a total of  or 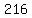 possible outcomes.
Look for the ten outcomes and for each value of the die see if it is still below six.
Any sums of 5 will be eliminated.
Any sums at 2 will still be under six for 1,2,and 3.
Any sums at 3 will still be under six for 1 and 2.
Any sums at 4 will still be under six for 1.
So adding the new die value as the first variable,
Sums of 2 getting updated to (using 1,2,3),
(1,1,1)
(2,1,1)
(3,1,1)
.
.
Sums of 3 getting updated to (using 1,2),
(1,1,2)
(2,1,2)
(1,2,1)
(2,2,1)
.
.
Sums of 4 getting updated to (using 1),
(1,1,3)
(1,2,2)
(1,3,1)
So that makes 10 outcomes out of 216 still under six.
|
|
|
