Question 1072879: A container contains 10 diesel engines. The company chooses 6 engines at random, and will not ship the container if any of the engines chosen are defective. Find the probability that a container will be shipped even though it contains 2 defectives if the sample size is 6.
Can someone please breakdown the steps to solve this. This is an online class and the help feature isn't explaining how to get the numbers needed to solve it. Thank you
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am baffled by the phrase "if the sample size is 6" at the end of the problem.
The problem said before that the company chooses 6 engines out of the 10 in the container. What is that phrase about sample size for?
Anyway, there are 
different possible sets of 6 engines that can be chosen.
NOTE: That is combinations of 10 taking 6 at a time.
Your online class may use a symbol with a  for combinations, for combinations,
instead of the 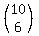 notation I used. notation I used.
There are only 
sets of 6 good engines that can be made with the
 good engines in that container that has good engines in that container that has  defective ones. defective ones.
As a fraction that is  , ,
and that is the probability that the set of 6 engines chosen does not have a defective one.
FORMULAS:
I do not like formulas as a substitute for understanding concepts.
The concept that is relevant to this problem is the concept of combinations.
The number ways of choosing a set of  engines engines
out of a set of  engines, can be seen as engines, can be seen as
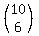 , the number of ways to pick the chosen , the number of ways to pick the chosen  , ,
or  , the number of ways of selecting the ( , the number of ways of selecting the ( not chosen. not chosen.
 , ,
with  factors in numerator, and factors in numerator, and  factors in denominator, factors in denominator,
makes for an easier calculation than
 . .
Below are the formulas and why they are the way they are.
Permutations of  items taking all items taking all  is is
the number of different ordered lists of  items that can be made items that can be made
from all  items of a set of items of a set of  different items is different items is
    , ,
because there are
 ways to pick the first item for the list, ways to pick the first item for the list,
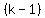 ways to pick the second item for the list, ways to pick the second item for the list,
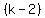 ways to pick the third item for the list, ways to pick the third item for the list,
and so on, until you have
 ways to pick one of the ways to pick one of the  items not picked before, items not picked before,
 ways to pick one of the ways to pick one of the  items not picked before, items not picked before,
and  choice for the last item on the list. choice for the last item on the list.
That 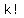 is the number of options a teacher would have is the number of options a teacher would have
to randomly line up all  students in a class. students in a class.
Permutations of  items taking items taking  of them is of them is
the number of different ordered lists of  items that can be made items that can be made
from the  different items in a set. different items in a set.
That number is

That is a product of  factors. factors.
That is the number of options a teacher would have to randomly select
a line of  of the of the  students in the school. students in the school.
The teacher would have
 choices for the first student in the line, choices for the first student in the line,
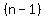 choices for the second student in the line, choices for the second student in the line,
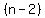 choices for the third student in the line, choices for the third student in the line,
and so on, until there are 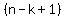 choices possible choices possible
for the last of the  picks. picks.
For the last of the  picks, picks,
there are 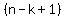 students wishing (or dreading) to be the last pick. students wishing (or dreading) to be the last pick.
(After that last pick, there are 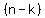 students left out, students left out,
disappointed, or relieved that they were not picked).
You can see how factors in the factorials ratio simplify leaving only  factors. factors.
 . .
Combinations of  items taking items taking  of them is of them is
the number of different sets of  items that can be made items that can be made
from the  different items in a set. different items in a set.
The formula for combinations of  taken taken  at a time is at a time is
 . .
It is the number of possible sets  of the of the  students in the school that can be made. students in the school that can be made.
There are 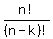 possible lists, possible lists,
but they are not going to be lined up, order does not matter.
Any  set of set of  students will be listed in a different order in students will be listed in a different order in 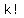 lists, lists,
but it is just  set, set,
so the 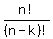 possible lists boil doen to possible lists boil doen to
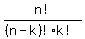 possible sets. possible sets.
|
|
|