SOLUTION: Find the value of {1}/{1 + {1}/{2 +{1}/{1 + {1}/{2 + ...}}}}

If I understand (guess) your problem correctly, you are asking about this infinite continued fraction


1
--------------------------
      1
1 + ----------------------
           1
      2 + ----------------
                 1 
           1 + -----------
                      1
                2 + ------
                        
                    1 + --


The standard way of solving such problems is THIS:


Let "x" be the value (now unknown) of this infinite continued fraction.

Then we can write the fraction in this form

      1 
x = ------------------------
            1  
      1 + ------------------
           2 + x

and it is just  an equation in the FINITE fraction form.

Simplify it using standard rules, and you will get

      2 + x                2 + x
x = ---------------  =  --------------
      (2 + x) + 1          3 + x

Multiply both sides by 3+x to rid of the denominator. You will get

x*(3+x) = 2 + x,

x^2 + 3x = 2 + x,

x^2 + 2x - 2 = 0,

 =  =  = .


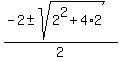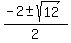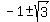Only positive solution works.

Therefore, x =  = 0.732051 . . . .

Approximately, x = 0.732051.