SOLUTION: yes how to solve: how many different 10 letter words (real or imaginary) can be formed from: s,f,s,m,z,s,f,a,i,n

 s,f,s,m,z,s,f,a,i,n

If the 3 s's and 2 f's looked different, maybe colored differently,
like this:

 s,f,s,m,z,s,f,a,i,n

then the number of distinguishable "words" would be 10!.

However there are many arrangements that we cannot tell apart 
because the 3 s's and 2 f's look just alike.

So we must divide the 10! by the product of the factorials
of the numbers of indistinguishable letters.

Since there are 3 indistinguishable s's and 2 indistinguishable f's,
we divide the 10! by 3!2!:

Answer: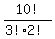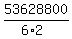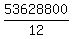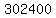 

Edwin