Question 1049339: There are 9! ways to arrange the digits 1-9 to form a 9-digit number. If you know this, then if you wrote all 9! possibilities on cards (1 way per card), and asked your friend to select one at random; what is the probability that the number he/she selected is prime?
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
There are 9! ways to arrange the digits 1-9 to form a 9-digit number. If you know this, then if you wrote all 9! possibilities on cards
(1 way per card), and asked your friend to select one at random; what is the probability that the number he/she selected is prime?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The probability is 0 (zero).
All these numbers (all and each of 9! numbers) are divisible by 3.
Each is a multiple of 3.
Apply the divisibility rule by 3.
The sum of all digits in each of these 9-digit numbers is
1 + 2 + 3 + . . . + 9 = 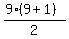 = 45
is divided by 3.
Thank you for this joke problem.
Good entertainment !
For divisibility rules see the lessons
- Divisibility by 2 rule,
- Divisibility by 3 rule,
- Divisibility by 4 rule,
- Divisibility by 5 rule,
- Divisibility by 6 rule,
- Divisibility by 9 rule,
- Divisibility by 10 rule,
- Divisibility by 11 rule,
- Restore the omitted digit in a number in a way that the number is divisible by 9 and
- Restore the omitted digit in a number in a way that the number is divisible by 11.
in this site.
|
|
|
