Question 1043953: Hello,I have tried approaching this question but don't know where to begin...
A school chess team consists of 10 students. In how many ways can a team of 6 students be formed for three consecutive games, if there should be a different line-up for each game?
Answer by ikleyn(52780)   (Show Source):
You can put this solution on YOUR website! .
Hello,I have tried approaching this question but don't know where to begin...
A school chess team consists of 10 students.
In how many ways can a team of 6 students be formed for three consecutive games, if there should be a different line-up for each game?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. As the first step, let us find how many 6-students teams can be formed of 10 students.
The answer i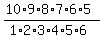s:  =  = 210.
At this moment I don't know if I should divide by the denominator.
If we must form a team each time, then I have to divide, and this formula is correct.
If we must to form a line each time (saying who is playing at the 1-st desk, who is playing at the 2-nd desc and so on)
- then I do not have to divide.
The condition does not allow me to choose between these options - at least as I understand the condition.
// So the condition is not ideal, by combining these terms "the team" and "line-up" in arbitrary way.
The ideal condition should point which of two versions works/is valid.
2. As the second, and final step, let us find in how many ways 3 different 6-student teams can be selected of the total
number of 210 different/distinguishable teams.
The answer is: in 210*209*208 = 9129120 ways.
The second opinion is desired.
But the major idea is clear: first find the number of teams/lines.
Then select three of the full number/amount.
|
|
|
