Prove Qn: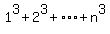 
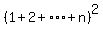First we will prove a well-known formula for the sum
of the first n positive integers:
Pn: 
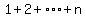
Then we can square both sides and get:
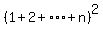
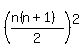then we will prove
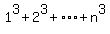
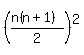Then what we are to prove will be immediate.
----------------------------------
First induction proof for
Pn: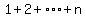
First let's see what Pk+1 would be:
[That's always the first thing to do. Before you
start an induction proof, you should calculate Pk+1
to see where you're headed]:
To do that, replace n by k+1 in 
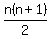to see
what the Pk+1 is, for that is what we are going for,
and if we have that beforehand, we'll know when we
have arrived and the proof is finished.
Substituting k+1 for n in 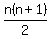, we have
or 
or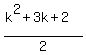 
Now that we know what Pk+1 is, we know where we're
going,
and we'll know we have arrived if and when we get
.
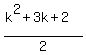So now we can start the proof:
P1: substitute n=1, 
, which is
clearly true.
Assume Pk: 
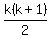Add (k+1) to both sides:
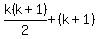
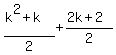
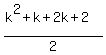
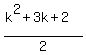and now we see that we get the same Pk+1 as the one
that we found in the beginning that we were going
for.
So the first proof is finished. Since P1 is true,
P1 proves P2, P2 proves P3, P3 proves P4, etc., etc.,
ad infinitum.
------------------
Now we prove
Qn: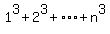
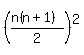As before, let's see what Qk+1 would be:
To do that, replace n by k+1 in 
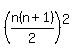to
see what the Qk+1 is. That is what we are going for,
and as before, if we have that beforehand, we'll know
when we have arrived and the proof is finished.
Substituting k+1 for n in 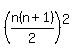, we have
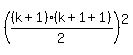or 
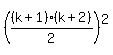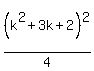or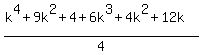 
or 
or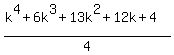 
Now that we know what Qk+1 is, we know where we're
going, and we'll know we have arrived if and when we
get .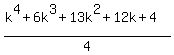
So now we can start the second proof:
Q1: substitute n=1, 
, which is clearly
true.
Assume Qk: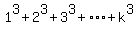 
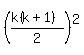Add (k+1)³ to both sides:
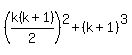
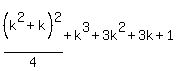
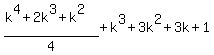
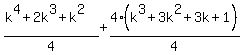
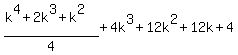
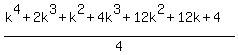
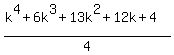and now we see that we get the same Qk+1 as the one
that we found in the beginning that we were going for.
So the second proof is finished. Since Q1 is true,
Q1 proves Q2, Q2 proves Q3, Q3 proves Q4, etc., etc.,
ad infinitum.
Edwin
