The following uses the five vowels (A,E,I,O,U).
What is the probability that when randomly selecting
a permutation of the 26 letters (assumed all uppercase)
of the alphabet the following events will occur:
A: The first 13 letters will be in alphabetical order.
It is obvious (to me) that the probability is 1/13!
But if not to you, then:
There are 52! arrangements of the letters of the alphabet.
Consider a sample such arrangement where the first 13
are in alphabetical order, say,
(1). BCDGHIJPQWXYZEMLNVRKAOSUFT
Among the 52!, there are 13! ways the first 13 letters
can be arranged, one such being, say,
(2). PIZDHBYGXCWJQEMLNVRKAOSUFT
Thus (1) is the only "successful" case out of the 13! cases
that include only the "successful" (1) and the other
"unsuccessful" cases such as (2).
Thus to get the number of ways the first 13 letters are in
alphabetical order, we must divide 52! by 13!
Thus the probability is 52!/13! ways out of 52! or
= 
-------------------------------
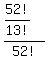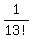E: The first and last letters will be B and Y.
That is 24!/26! = 1/(26*25) = 1/650,
for there are 24! ways to arrange the other 24
letters between B on the far left and Y on the
far right.
B _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ Y
-------------------------------
I: The letter I will come before both J and K.
Look at these 3! or 6 arrangements of the 26 letters:
PIZDHBYGXCWJQEMLNVRKAOSUFT
PIZDHBYGXCWKQEMLNVRJAOSUFT
PJZDHBYGXCWIQEMLNVRKAOSUFT
PKZDHBYGXCWIQEMLNVRJAOSUFT
PJZDHBYGXCWKQEMLNVRIAOSUFT
PKZDHBYGXCWJQEMLNVRIAOSUFT
Only the first 2 out of those 6 ways does I come before
both J and K. Thus the probability is 2/6 or 1/3
-----------------
O: The letters O and P will be next to each other.
That's the 25! arrangements of these 25 things,
consisting of 24 single letters and 1 letter pair:
A,B,C,D,E,F,G,H,I,J,K,L,M,N,(OP),Q,R,S,T,U,V,W,X,Y,Z
plus the 25! arrangements of these 25 things,
also consisting of 24 single letters and 1 letter pair:
A,B,C,D,E,F,G,H,I,J,K,L,M,N,(PO),Q,R,S,T,U,V,W,X,Y,Z
So the probability is 2(25!/26!) = 2(1/26) = 1/13
-------------------
U: The letters U and V will be separated by at least 23 letters.
There are the 6 ways indicated below to place the U and V,
and 24! ways of arranging the other 24 letters.
U _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ V _
U _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ V
_ U _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ V
V _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ U _
V _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ U
_ V _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ U
6(24!)/(26!) = 6[1/(26*25)] = 6/(26*25) = 3(13*25) = 3/325
Edwin
