Question 1037588: In how many ways can the letters of the word irrational be arranged
Answer by purpleoj(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! The answer depends on whether you need just the amount of possible ways or whether they need to be distinguishable.
You calculate the number of possible ways by simply writing 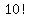 , which, in expanded form, means , which, in expanded form, means 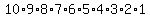 , which equals 3628800, which is your number of possible ways. , which equals 3628800, which is your number of possible ways.
However, because there are three instances of the same letter (there are 2 "a"s, 2 "r"s, and 2 "i"s), you must divide by the factorial of number of times each letter occurs seperately to make each way distinguishable, otherwise you will have identical looking combinations of letters.
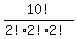
This will give you 453600.
Your two answers will be 3628800 for a nondistinguishable permutation, or 453600 for a distinguishable permutation.
|
|
|