Question 1035206: Let S be a set with eleven elements. How many 4 element subsets does S have? How many ordered triples (x,y,z) are there belonging to S x S x S such that no two of x, y, and z are equal? Give answers in terms of combination symbols or products (no arithmetic)
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
Let S be a set with eleven elements. How many 4 element subsets does S have? How many ordered triples (x,y,z) are there
belonging to S x S x S such that no two of x, y, and z are equal? Give answers in terms of combination symbols or products (no arithmetic)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. How many 4 element subsets does S have?
Answer.  =  =  .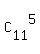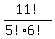
2. How many ordered triples (x,y,z) are there belonging to S x S x S such that no two of x, y, and z are equal?
Hint:
First calculate the total number of elements in S x S x S.
It is  .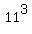
Next, calculate the number of triples (x,y,z), where at least two of three elements x, y and/or z are identical.
Avoid calculating the same triples twice!
Then distract the second number from the first.
|
|
|
