SOLUTION: Cakes cost $8 each and pies cost $6 each. How many combinations of cakes and pies can you purchase for between $72 and $120, inclusive?

Let x = the number of cakes and y = the number of pies.
x and y must be non-negative integers.  A "lattice point" 
is a point both of whose coordinates are integers, in this 
case only non-negative integers.  The inequality is



Or, dividing through by $2,



We graph the set of inequalities:  



The solution set is the number of lattice points interior to
or on the sides of trapezoid ABCD.

Notice that the line 4x+3y=36, which is AD and the line 
4x+3y=60 which is BC are the respective diagonals of the 
rectangles AODE and BOCF in the figure
 








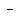
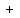
We first find the number of lattice points on the
two diagonals BC and AD 

We find the points on 
diagonal BC
The equation of BC is 

Write 4x as 3x+x

Divide through by 3

Isolate the fraction term

The right side is a non-negative integer,
therefore so is the left side.  Let that
integer by p, then





So the diagonal lattice points on AD are 
(3p,12-4p) where p = 0,1,2,3
Thus there are 4 lattice points on diagonal BC

We find the number of lattice points on diagonal
AD:
The equation of AD is 

Write 4x as 3x+x

Divide through by 3

Isolate the fraction term

The right side is a non-negative integer,
therefore so is the left side.  Let that
integer by q, then






So the lattice points on AD are (3p,20-4q) 
where q = 0,1,2,3,4,5

Thus there are 6 lattice points on diagonal AD.

Next we find the number of lattice points with 
non-negative coordinates below the line BC.
There are 10x13 = 130 lattice points in or on
the rectangle BOCF.  That's because the lattice
points on OC go from 0 through 9, which is 10
lattice points. Also, the lattice points go from 
0 through 12 on OB, which is 13 lattice points
along the left side.

By symmetry, there are the same number of lattice 
points in rectangle BOCF above the diagonal of AD,
as there are below it.

The number of lattice points in or on rectangle 
AODE above or below but not on diagonal AD is 130-4=126.
So there are 126/2 = 63 latice points below AD.

Next we find the number of lattice points with 
non-negative coordinates below the line AD.
There are 16x21 = 336 lattice points in or on
the rectangle AODE.  That's because the lattice
points on OD go from 0 through 15, which is 16,
and from 0 through 20 on AO, which is 21.
By symmetry. there are the same number of lattice 
points above the diagonal AD in rectangle AODE, 
as there are below it.

The number of lattice points in or on rectangle 
AODE above or below the diagonal AD is 336-6=330.
So there are 330/2 = 165 lattice pointsin rectangle
AODE below AD. 

However we want only the non-diagonal lattice points 
and the 165 includes the 4 diagonal points on BC.  So
we must subtract those 4 from the 165, which leaves
161 non-diagonal points below AD. 

So we substitute in
 








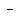
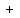
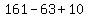Answer: 

Edwin