SOLUTION: There are 11 guests in a party 1)In how many ways can the guests be seated at a round table with 15 numbered seats? 2)In how many ways can the guests be seated at a round table w

Algebra ->  Permutations -> SOLUTION: There are 11 guests in a party 1)In how many ways can the guests be seated at a round table with 15 numbered seats? 2)In how many ways can the guests be seated at a round table w      Log On


   

Question 1024774: There are 11 guests in a party
1)In how many ways can the guests be seated at a round table with 15 numbered seats?
2)In how many ways can the guests be seated at a round table with 15 identical seats?
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
There are 11 guests in a party
1)In how many ways can the guests be seated at a round table with 15 numbered seats?
2)In how many ways can the guests be seated at a round table with 15 identical seats?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

1.  The first guest can choose any of 15 seats.
    The second guest can choose any of 14 remaining seats.
    . . . . 
    The 11-th guest can choose any of (15-10) = 5 seats.

    In all, there are 15*14*13* . . . *5 = 15%21%0D%0A%2F4%21 ways/options.


2.  If the seats are non-numbered (i.e. identical), we can not and do not make distinguish 
    between configurations that differ by the turning / circular translation of all seats around the table 
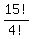    in 1, 2, 3, . . . , 15 positions. So, we need to divide 15%21%2F4%21 by 15.

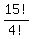    Thus the answer is 1%2F15.15%21%2F4%21 = 14*13*12* . . . *5.