First we find the number of distinguishable permutations of
ARRANGEMENT. There are 2 A's, 2 R's, 2 E's, and 2 N's. So
that's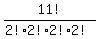 
From that we must subtract the number of distinguishable
permutations in which the A's, R's or both come together.
We use the "sieve" formula:
N(X or Y) = N(X) + N(Y) - N(X and Y)
where N() means "the number of elements of".
N(permutations with A's together OR R's together) =
N(permutations with A's together) +
N(permutations with R's together) -
N(permutations with A's together AND R's together)
-------
Let's get this first: N(permutations with A's together)
They are the distinguishable arrangements of these
10 things:
(AA),R,R,N,G,E,M,E,N,T
There are 2 R's, 2 N's, 2 E's, but only one (AA)
That's 
---
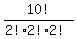
Let's get this next: N(permutations with R's together)
They are the distinguishable arrangements of these
10 things:
{A,A,(RR),N,G,E,M,E,N,T}
That's also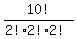
---
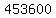Now we get: N(permutations with A's together AND R's together)
They are the distinguishable arrangements of these
9 things:
(AA),(RR),N,G,E,M,E,N,T
There are 2 N's, and 2 E's, but only one (AA) and one (RR)
That's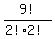 
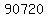So the number we must subtract from the 2494800 is
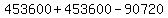
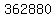So the final answer is
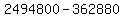
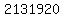Edwin
