For PERMUTATIONS, we PLACE in POSITIONS.
For COMBINATIONS, we merely CHOOSE, we don't place them in positions.
P for permutations, P for Placing in POSITIONS.
C for combinations, C for CHOOSING
There are 5 students in a small class.
To make a team, the names of 3 of them will be drawn from a hat.
How many different teams of 3 students are possible?
We are merely CHOOSING them, not POSITIONING them, so its
COMBINATIONS.
5 students CHOOSE 3 = 5C3 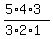 =
= 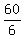 = 10.
Suppose the 5 students are A,B,C,D,E. The 10 ways to choose 3 are
1. {A,B,C}
2. {A,B,D}
3. {A,B,E}
4. {A,C,D}
5. {A,C,E}
6. {A,D,E}
7. {B,C,D}
8. {B,C,E}
9. {B,D,E}
10. {C,D,E}
Edwin
= 10.
Suppose the 5 students are A,B,C,D,E. The 10 ways to choose 3 are
1. {A,B,C}
2. {A,B,D}
3. {A,B,E}
4. {A,C,D}
5. {A,C,E}
6. {A,D,E}
7. {B,C,D}
8. {B,C,E}
9. {B,D,E}
10. {C,D,E}
Edwin