Question 1006522: Cuold you please help me understand what formula to use for this problem?
A warehouse employs 24 workers on first shift and 17 workers on second shift. Eight workers are chosen at random to be interviewed about the work enviironment. Find the probability of choosing six first-shift workers.
I tried this formula: 24C6*17C2/41C8. The textbook shows the answer to be .192, but I could find no examples of this type of problem.
Thank you for your help.
Found 3 solutions by MathLover1, Boreal, KMST:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by Boreal(15235)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If this does not fully explain what you did not learn or did not understand, feel free to ask me via a thank you note in this website.
There is a total of  workers. workers.
There are  possible different sets of possible different sets of  workers that can be made from those workers that can be made from those  workers. workers.
Some of those  sets will have sets will have
 of the of the  workers on first shift and workers on first shift and
 of the of the  workers on second shift. workers on second shift.
How many such sets are possible?
Since there are
 possible different sets of possible different sets of  workers that can be made from the workers that can be made from the  workers on first shift and workers on first shift and
 possible different sets of possible different sets of  workers that can be made from the workers that can be made from the  workers on second shift, workers on second shift,
there are 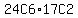 possible different sets of possible different sets of  workers made up of exactly workers made up of exactly  workers from first shift and workers from first shift and  workers from second shift. workers from second shift.
Those 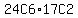 sets are sets are 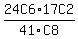 of the total of the total 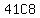 possible sets of possible sets of  workers, workers,
and that fraction is the probability of getting exactly  workers from first shift and workers from first shift and  workers from second shift: workers from second shift:
 
CAUTION:
Beware of a common mistake.
If you try entering that calculation into your calculator, you must enter
95548245 / ( 134596 X 136 ) =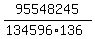 or or
95548245 / 134596 / 136 = , ,
because that long horizontal line between  and and 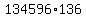
means that 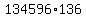 must be calculated first, so in other words must be calculated first, so in other words
that line implies the parentheses around 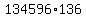 . .
If you do not enter the parentheses, you are doing the indicated operations in order from left to right:
you are first dividing by 134596,
and then multiplying the result times 136, so you get
95548245 / 134596 X 136 = (rounded) , (rounded) ,
which is ridiculous, because probabilities cannot be more than 1.00.
|
|
|