Question 914497: The ratio of the areas of 2 squares is 6:7. If the perimeter of the larger square is 73.5 what is the perimeter of the smaller aquare? Please help me solve them. Thank youuuu so much 😊😊😊
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the side lengths of the smaller and larger squares are  and and  respectively, respectively,
the perimeters are 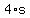 and and 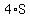 respectively, respectively,
with 
The ratio of their sides and perimeters is  , ,
and the ratio of their areas is 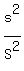 . .
We know that  . .
 --> --> --> --> --> -->
So,  ---> ---> (rounded). (rounded).
NOTES:
In general, when you have similar shapes (same figure, or 3-D solid, but scaled up or down),
if the ratio of length measures (side lengths, perimeters, circumferences, etc) is  , ,
then the ratio of the corresponding areas is 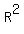 , ,
and (if the similar shapes are 3-dimensional) the ratio of the volumes is  . .
The larger square is a scaled up version of the smaller square, so that applies.
(We could not say the same of triangles, or rectangles).
|
|
|