Question 833572: Kate has found six two-digit numbers, such that no three of them can constitute the lengths of a triangle's sides.Can you find such a number?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! My numbers are  , ,  , , 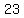 , ,  , ,  , and , and 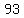 . .
If 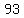 were the length of the longest side, to form a triangle, the lengths of the other two sides must add up to more than were the length of the longest side, to form a triangle, the lengths of the other two sides must add up to more than 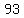 , but I chose the numbers so that , but I chose the numbers so that  is equal to or greater than the sum of any two of the other numbers. is equal to or greater than the sum of any two of the other numbers.
Each of the numbers  , ,  , and , and 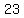 , cannot be the measure of the longest side for a similar reason: , cannot be the measure of the longest side for a similar reason:
 , ,  , and , and  . .
|
|
|