|
Question 49107: In a certain class, 1/3 of the girls are 1/5 if tge students. What is the ratio of boys to girls in the class?
I know that they have more boys, can you help.
Thanks!
Answer by Born2TeachMath(20)   (Show Source):
You can put this solution on YOUR website! Actually, you're wrong! There are more girls than boys, but it doesn't sound like it, does it?
You can play around with variables, and "let g = # of girls", etc. but that's not the way to do this.
It says that 1/3 of the girls are 1/5 of the students. That means that the next 1/3 of the girls is another 1/5 of the students, and the last 1/3 of the girls are yet another 1/5 of the students. Therefore, if you combine all three 1/3's of the girls, that must be all of the girls. This also accounts for 1/5 + 1/5 + 1/5 = 3/5 of the students. So the girls are 3/5 of the students, which means the boys must be the other 2/5 of the students. So to find a ratio, express it as a fraction of boys on top with fraction of girls on bottom. This becomes 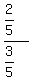 . Now, if you remember how to divide fractions, you flip the bottom fraction over, and then multiply the two together:  . Remember, when multiplying fractions, don't actually multiply the numbers out - just cancel the 5 on the top with the 5 on the bottom, and the fraction becomes  . Since we put the boys on the top, the answer to your problem is 2 to 3 for boys to girls.
Look, more girls than boys!!
|
|
|
| |
