|
Question 1210396: Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5 of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the cost of a muffin?
Found 3 solutions by greenestamps, mccravyedwin, MathTherapy:
Answer by greenestamps(13219)   (Show Source): (Show Source):
Answer by mccravyedwin(411)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Most tutors, including me, often ignore where it says this:
"Also, if possible, provide a 'check' at the end, so check if the values
you computed in fact are correct".
Nearly always, we skip this check.
If we would read and heed that, then perhaps we might use a different
method, to make it easier to check.
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5
of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as
a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the
cost of a muffin?
Let T = total money Hakim had at the beginning.
Let C = cost of a cupcake
Let M = cost of a muffin
Let W = cost of a piece of waffle
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
 Then he spent 4/5 of the remaining money
which was
Then he spent 4/5 of the remaining money
which was 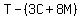 on 15 pieces of waffle.
on 15 pieces of waffle.
 Each cupcake cost 2/3 as much as a muffin.
Each cupcake cost 2/3 as much as a muffin.
 Each piece of waffle cost $0.20 more than a cupcake.
Each piece of waffle cost $0.20 more than a cupcake.

 Go to any of the online solvers for systems of equations
https://www.wolframalpha.com/
https://www.symbolab.com/solver/system-of-equations-calculator
https://cowpi.com/math/systemsolver/4x4.html
https://www.wolframalpha.com/calculators/system-equation-calculator
There are others also.
Type in
(3/8)T = 3C + 8M, (4/5)(T-(3C+8M))=15W, C = (2/3)M, W = C+0.20
Press ENTER, get
C = 0.6, M = 0.09, T = 24, W = 0.8
which we interpret as
C = $0.60, M = $0.90, T = $24.00, W = $0.80.
What was the cost of a muffin?
$0.90 <--- solved, but not checked.
Now let's check:
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
(3/8)x$24.00 = $9.00
3x$0.60 = $1.80, 8x$0.90 = $7.20, $1.80 + $7.20 = $9.00.
That checks.
So his remaining money was $24.00 - $9.00 = $15.00
Then he spent 4/5 of the remaining money
which was (4/5)x$15.00 = $12.00
on 15 pieces of waffle.
15x$0.80 = $12.00 and, indeed, that checks.
Each cupcake cost 2/3 as much as a muffin.
$0.60 = (2/3)($0.90)
$0.60 = $0.60, so that checks.
Each piece of waffle cost $0.20 more than a cupcake.
$0.80 = $0.60 + $0.20
$0.80 = $0.80, so that checks.
Now, as you see, everything checks.
Edwin
Go to any of the online solvers for systems of equations
https://www.wolframalpha.com/
https://www.symbolab.com/solver/system-of-equations-calculator
https://cowpi.com/math/systemsolver/4x4.html
https://www.wolframalpha.com/calculators/system-equation-calculator
There are others also.
Type in
(3/8)T = 3C + 8M, (4/5)(T-(3C+8M))=15W, C = (2/3)M, W = C+0.20
Press ENTER, get
C = 0.6, M = 0.09, T = 24, W = 0.8
which we interpret as
C = $0.60, M = $0.90, T = $24.00, W = $0.80.
What was the cost of a muffin?
$0.90 <--- solved, but not checked.
Now let's check:
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins.
(3/8)x$24.00 = $9.00
3x$0.60 = $1.80, 8x$0.90 = $7.20, $1.80 + $7.20 = $9.00.
That checks.
So his remaining money was $24.00 - $9.00 = $15.00
Then he spent 4/5 of the remaining money
which was (4/5)x$15.00 = $12.00
on 15 pieces of waffle.
15x$0.80 = $12.00 and, indeed, that checks.
Each cupcake cost 2/3 as much as a muffin.
$0.60 = (2/3)($0.90)
$0.60 = $0.60, so that checks.
Each piece of waffle cost $0.20 more than a cupcake.
$0.80 = $0.60 + $0.20
$0.80 = $0.80, so that checks.
Now, as you see, everything checks.
Edwin
Answer by MathTherapy(10560)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hakim spent 3/8 of his money on 3 cupcakes and 8 muffins. Then he spent 4/5 of the remaining money on 15 pieces of waffle. Each cupcake cost 2/3 as much as a muffin. Each piece of waffle cost $0.20 more than a cupcake. What was the cost of a muffin?
Let amount spent, be D, cost of a muffin, M, and cost of a cupcake. C
For the first purchase, we get:  3D = 24C + 64M ---- Multiplying by LCD, 8 ---- eq (i)
For the second purchase, we get:
3D = 24C + 64M ---- Multiplying by LCD, 8 ---- eq (i)
For the second purchase, we get:


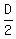 = 15W ---- eq (ii)
Each cupcake cost = 15W ---- eq (ii)
Each cupcake cost  as much as a muffin, so: C = as much as a muffin, so: C =  ---- eq (iii)
Each piece of waffle cost $0.20 more than a cupcake, so: W = ---- eq (iii)
Each piece of waffle cost $0.20 more than a cupcake, so: W = 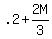 ---- eq (iv) ---- eq (iv)
 ------ eq (ii) ------ eq (ii)
 ---- Substituting ---- Substituting 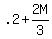 for W, in eq (ii) for W, in eq (ii)
 D = 6 + 20M ---- Multiplying by LCD, 2 ---- eq (v)
3D = 24C + 64M ------ eq (i)
D = 6 + 20M ---- Multiplying by LCD, 2 ---- eq (v)
3D = 24C + 64M ------ eq (i)
 --- Substituting --- Substituting 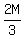 for C, in eq (i)
3D = 8(2M) + 64M
3D = 16M + 64M
3D = 80M ---- eq (vi)
D = 6 + 20M ---- eq (v)
3D = 80M ---- eq (vi)
3D = 18 + 60M ---- Multiplying eq (v) by 3 ---- eq (vii)
0 = - 18 + 20M --- Subtracting eq (vii) from eq (vi)
- 20M = - 18
Cost of a muffin, or for C, in eq (i)
3D = 8(2M) + 64M
3D = 16M + 64M
3D = 80M ---- eq (vi)
D = 6 + 20M ---- eq (v)
3D = 80M ---- eq (vi)
3D = 18 + 60M ---- Multiplying eq (v) by 3 ---- eq (vii)
0 = - 18 + 20M --- Subtracting eq (vii) from eq (vi)
- 20M = - 18
Cost of a muffin, or 
|
|
|
| |