|
Question 1206592: Every month. Andie spent 1/5 of his salary on food and 2/3 of the remaining salary on transport. After spending his salary on food and transport, he gave 50% of the rest of the salary to his parents and saved the rest of the $350 How much did he spend on food and transport every month?
Found 3 solutions by greenestamps, ikleyn, MathTherapy:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The poor wording allows for different interpretations of the given information.
"... he gave 50% of the rest of the salary to his parents and saved the rest of the $350..."
The best interpretation of that exact wording is that he had $350 left after food and transportation, of which he gave 50% to his parents.
But it could also be interpreted as saying that $350 is the amount he saved.
The tutors here (most of them, anyway) are not going to spend time trying to help you with the problem if they don't know for sure what the given information is.
Clean up the wording and re-post.
--------------------------------------------------------
Added after seeing the response from tutor @ikleyn....
The backwards method of solving problems like this is useful, and for many problems similar to this one it is easier to use. It is especially useful if the steps say things like "he spent 1/5 of his salary plus $40 on food...".
However, in this problem, all the steps are just using certain fractions or percentages of the remaining amounts, without any of those "... plus $40..." phrases. That makes solving the problem "forwards" easier than solving it backwards.
He spent 1/5 of his salary on food; the fraction he has left is 4/5.
He then spent 2/3 of that 4/5 of his salary on transportation, so what he has left is 1/3 of 4/5 of his salary, or 4/15 of his salary.
He then gave 50% (1/2) of what he had left to his parents, so what he had left was 1/2 of 4/15 of his salary, or 2/15 of his salary. So he saved 2/15 of his salary.
Now we come to the problem with the exact wording of the problem.
If the problem said he saved "THE REMAINING $350", it would mean that he gave his parents $350 and saved the last $350.
But the problem says "...he gave 50% of the REST OF THE salary to his parents and saved the REST OF THE $350". Grammatically, that means the $350 is what was left after he paid for food and transportation, and that he gave half of it to his parents and saved the other half. So the amount he saved was $175 -- NOT $350.
He spent 1/5 = 3/15 of his salary on food.
He spent 8/15 of his salary on transportation.
He gave 2/15 of his salary to his parents.
He saved 2/15 of his salary.
The total he spent on food and transportation was 11/15 of his salary. That is 11/2 of what he saved.
If the amount he saved was $350 (grammatically incorrect), then the amount he spent on food and transportation was (11/2)$350 = $1925.
If the amount he saved was $175 (grammatically correct), then the amount he spent on food and transportation was (11/2)$175 = $962.50.
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Every month. Andie spent 1/5 of his salary on food and
2/3 of the remaining salary on transport.
After spending his salary on food and transport, he gave 50% of the rest of the salary to his parents
and saved the rest of the $350 How much did he spend on food and transport every month?
~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the Andie's total salary.
Make this table
(line 1) 1/5 of x is spent on food. The remainder is R1 = 4/5*x.
(line 2) 2/3 of R1 is spent on transport. The remainder is R2 = (1/3)*R1.
(line 3) 0.5 of R2 is given to parents. The remaining $350 go to saving.
Let' start analyze from the last line 3.
From the table, from its line 3, the remainder of $350 for saving is the same amount as given to parents.
So, $350 is given to parents.
Thus R2 is twice $350, or $350 + $350 = $700.
Next, from the table, from its line 2, R2 is 1/3 of R1.
R2 is $700, as we found out in line 3. Hence, R1 is 3 * $700 = $2100.
2/3 of R1 is 2/3 * 2100 = $1400. It is the amount for transport.
Now let's analyze in line 1.
R1 is $2100, as we found out in line 2.
R1 is 4/5 of x. Hence, x is 5/4*2100 = 2625 dollars and the spending on food is 1/5 * 2625 = 525 dollars.
Thus spending on food and transport together is $1400 + $525 = $1925. ANSWER
CHECK. Total salary is $2625.
1/5 is spent on food, 1/5 * 2625 = 525 dollars. The remainder is R1 = $2625 - $525 = $2100.
2/3 of R1 is spent on transport. 2/3 of $2100 is $1400, The remainder R2 = $2100 - $1400 = $700.
The remainder R2 = $700 is split evenly between parents and saving. ! correct !
Solved.
---------------
I solved this problem using a backward method.
It allows restore unknowns step by step MENTALLY, moving backward
from the end to the beginning, without using equations.
I consciously did not use the method of making and solving equations here,
since my goal was to make you familiar with this BACKWARD method.
|||||||||||||||||||||||||||||||||||
It is useful to know and to understand the following fact.
If your approach to solving the problem is making and solving equations, then the technical difficulties
of constructing these equations will quickly increase with increasing the number of subdivisions
(of the length of the chain) in this problem.
But if your approach is a backward method, then it is almost the same, if the length of the chain
is 5, or 10, or 20. The formal algorithm of the backward method remains the same, with no changes.
The backward method remains robust even for long chains of subdivisions (!)
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Every month. Andie spent 1/5 of his salary on food and 2/3 of the remaining salary on transport. After spending his salary on food and transport, he gave 50% of the rest of the salary to his parents and saved the rest of the $350 How much did he spend on food and transport every month?
After spending  on food, on food, 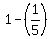 , or , or  of his salary remained
After spending of his salary remained
After spending  of REMAINDER on transportation, of REMAINDER on transportation, 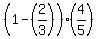 or or  of his salary remained
After giving 50% (.5) of the remaining of his salary remained
After giving 50% (.5) of the remaining 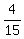 to his parents, he had .5( to his parents, he had .5(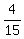 ), or ), or  remaining, which happens to be $350
Since remaining, which happens to be $350
Since 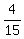 of his salary remained after spending some on food and transportation, of his salary remained after spending some on food and transportation, 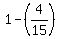 , or , or 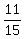 of his salary was
spent on food and transportation
This then produces the following PROPORTION: of his salary was
spent on food and transportation
This then produces the following PROPORTION:  , with x being the amount spent on food and transportation , with x being the amount spent on food and transportation
 2x = 11(350) ---- Cross-multiplying
Amount spent on food and transportation, or
2x = 11(350) ---- Cross-multiplying
Amount spent on food and transportation, or 
|
|
|
| |