|
Question 1205102: Eli Al’s has a collection of marbles. If he gives away 3/5 of his marbles to his friend and then buys 20 more marbles, he will have 100 marbles in total. How many marbles did Eli Al have originally?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
Eli Al’s has a collection of marbles. If he gives away 3/5 of his marbles to his friend
and then buys 20 more marbles, he will have 100 marbles in total.
How many marbles did Eli Al have originally?
~~~~~~~~~~~~~~~~~~~~~~
Good problem to solve it MENTALLY by a BACKWARD method.
+----------------------------------------------------------------+
| We start from the end and move backward to the beginning |
| step by step, using reasoning and making simple arithmetic. |
| No equations are needed, so this method is good even for |
| 4-th grade young students of primary schools. |
+----------------------------------------------------------------+
At the end, Eli Al has 100 marbles.
Hence, immediately before he bought 20 marbles, he had 100-20 = 80 marbles.
Hence, these 80 marbles were  =  of marbles he had initially.
Hence, initially he had 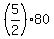 = 5*40 = 200 marbles.
ANSWER. Initially, Eli Al had 200 marbles.
Solved.
---------------------
To see many other similar and different solved problems, look into the lesson
Simple arithmetic word problems to solve by a backward method
in this site.
Learn the method from there.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
x = number of marbles he started with
(3/5)x = number of marbles given away
(2/5)x = number of marbles he keeps
(2/5)x+20 = amount after buying 20 more marbles
(2/5)x+20 = 100
(2/5)x = 100-20
(2/5)x = 80
x = 80*(5/2)
x = 200
Another way to solve
(2/5)x+20 = 100
5*( (2/5)x+20 ) = 5*100
5*(2/5)x + 5*20 = 500
2x + 100 = 500
2x = 500 - 100
2x = 400
x = 400/2
x = 200
Check:
He started with 200 marbles.
3/5 of which is (3/5)*200 = 0.6*200 = 120
He gives away 120 marbles and keeps 200-120 = 80. Note how (2/5)*200 = 0.4*200 = 80.
Then he buys 20 marbles to get 80+20 = 100 total at the end. We have confirmed the answer.
Another way to check:
(2/5)x+20 = 100
(2/5)*200+20 = 100
0.4*200+20 = 100
80+20 = 100
100 = 100
|
|
|
| |
