|
Question 1189654: Tony and Peter both had some marbles at first. After Tony gave Peter 4/14 of his marbles, the ratio of Tony’s marbles to Peter’s marbles became 5:3. What was the ratio of Peter’s marbles to Tony’s marbles at first?
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Before plunging into a "standard" algebraic solution, take the time to analyze the problem to see if there is an easier way to set the problem up.
At the start of the problem, Tony gave Peter 4/14=2/7 of his marbles; that means the number of marbles Tony started with was a multiple of 7. So
Let 7x = # of marbles Tony started with.
The number of marbles he gave to Peter was then 2x; the number Tony was left with was 5x.
After Tony gave those marbles to Peter, the ratio of marbles the two of them had was 5:3. So, since Tony finished with 5x marbles, Peter finished with 3x marbles.
2x of the marbles Peter finished with were what Tony gave him; since Peter finished with 3x marbles, he started with x marbles.
So Tony started with 7x marbles and Peter started with x marbles.
ANSWER: The ratio of Peter's marbles to Tony's marbles at first was x:7x = 1:7
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Tony and Peter both had some marbles at first. After Tony gave Peter 4/14 of his marbles,
the ratio of Tony’s marbles to Peter’s marbles became 5:3.
What was the ratio of Peter’s marbles to Tony’s marbles at first?.
~~~~~~~~~~~~~~~~
For me, it is psychologically difficult to see (to read) so long solution for so simple problem.
So, I came to bring a shorter solution (thinking that longer solution does not help understanding).
Finally, Tony has 5x marbles, while Peter has 3x marbles, where x is the common measure.
Let P = # of marbles Peter had initially;
T = # of marbles Tony had initially.
Then we have these equations
3x = P + 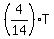 (1)
5x = (1)
5x = 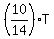 (2)
From equation (2), x = (2)
From equation (2), x =  = = 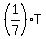 .
Substitute it into equation (1) to get .
Substitute it into equation (1) to get
 = P + = P + 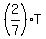 .
So, P = .
So, P = 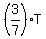 - - 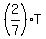 = = 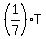 .
It means that .
It means that 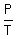 = =  . ANSWER . ANSWER
Solved.
//////////////
My conception is this: everything which is longer than 5 lines of standard text, is not a Math problem.
If a standard/regular school Math problem is given, than its solution should be no longer than 10 - 15 lines of the text; maximum 20 lines.
If a problem is exceptional, its solution may require "more lines" - it depends and it can be justified.
But if the solution to a regular/standard school Math problem is longer than 20 lines, then nobody even will read it . . .
|
|
|
| |