SOLUTION: Anton, Chris and Eddie had some tickets to sell for their school concert. After Anton sold 1/3 of his tickets, Chris sold 2/5 of his and Eddie sold 3/4 of his, they had an equal nu

Let 3x be the number of tickets Anton had initially;  then he sold   x  tickets and has  2x  tickets left.

    
Let 5y be the number of tickets Chris had initially;  then he sold  2y  tickets and has  3y  tickets left.


Let 4z be the number of tickets Eddie had initially;  then he sold  3z  tickets and has   z  tickets left.


From the condition, we have these equations


    2x = z               (1)

    3y = z               (2)

    x + 2y + 3z = 225    (3)


From (1), exoress x = z/2  and substitute into equation (3);  from (2), express y = z/3 and substitute into equation (3).

Then equation (3) takes the form


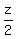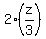     +  + 3z = 225.


Multiply both sides by 6 (all the terms); then simplify and find z


    3z + 4z + 18z = 6*225

         25z      = 6*225

           z  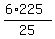    =  = 6*9 = 54.


So, according to the condition, each boy has 54 tickets left.    ANSWER