SOLUTION: The denominator of a fraction is three more than twice the numerator. If both numerator and denominator are decreased by five, the simplified result is 25. Find the original fracti

Algebra ->  Percentage-and-ratio-word-problems -> SOLUTION: The denominator of a fraction is three more than twice the numerator. If both numerator and denominator are decreased by five, the simplified result is 25. Find the original fracti      Log On


   

Question 1148071: The denominator of a fraction is three more than twice the numerator. If both numerator and denominator are decreased by five, the simplified result is 25. Find the original fraction. (Do NOT simplify.)
Answer by ikleyn(52835) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let x be the numerator.

Then the denominator is  2x+3, according to the condition.


Hence, the original fraction is 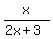 x%2F%282x%2B3%29.


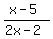The modified fraction is  %28x-5%29%2F%28%282x%2B3%29-5%29 = %28x-5%29%2F%282x-2%29, and you are given that  it is  25.


It gives you an equation


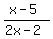    %28x-5%29%2F%282x-2%29 = 25.


It implies


    x - 5 = 50x - 50

    50-5 = 50x-x

    45   = 49x

    x    = 45%2F49


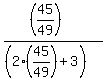ANSWER.  The original fraction is  %28%2845%2F49%29%29%2F%28%282%2A%2845%2F49%29%2B3%29%29.


         Since the problem instructs me "DO NOT SIMPLIFY", I should stop at this point.


My personal opinion is that most of such problems violate the notions and the rules of arithmetic and contradict them.