SOLUTION: Quadrilateral ABCD is a rhombus. Find X, Y, z, and the perimeter of ABCD measure of angle BCD=106 degrees measure of angle ADB= (4y+5) degrees measure of angle BAC= (6x-7) de

Algebra ->  Parallelograms -> SOLUTION: Quadrilateral ABCD is a rhombus. Find X, Y, z, and the perimeter of ABCD measure of angle BCD=106 degrees measure of angle ADB= (4y+5) degrees measure of angle BAC= (6x-7) de      Log On


   

Question 947419: Quadrilateral ABCD is a rhombus. Find X, Y, z, and the perimeter of ABCD
measure of angle BCD=106 degrees
measure of angle ADB= (4y+5) degrees
measure of angle BAC= (6x-7) degrees
EC=6
ED=5z-7
BE= 3z-1
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
It is not absolutely necessary to sketch the rhombus,
but it would help visualize the relations between angles.

Angles BCD and BAD are opposite angles, so they have the same measure:
BAD=DCD=106%5Eo .
Angle BAC (with side BA and diagonal AC) is half of angle BAD,
so BAC=BAD%2F2=BCD%2F2=106%5Eo%2F2=53%5Eo .
Without the drawing, I can tell that
ADB is one of the base angles of isosceles triangle ADB
(with diagonal BD as its base,
and angle BAD as its vertex angle),
so ADB=%28180%5Eo-BAD%29%2F2=%28180%5Eo-106%5Eo%29%2F2=74%5Eo%2F2=37%5Eo .
With the drawing, you can tell that
since the diagonals of a rhombus are perpendicular to each other,
angles ADB and BAC are acute angles in a right triangle,
and therefore complementary, so ADB=90%5Eo-BAC=90%5Eo-53%5Eo=37%5Eo .

With the angle measures in hand, the equations to find x and y are:
4y%2B5=37 and 6x-7=53
4y%2B5=37-->4y=37-5-->4y=32-->y=32%2F4-->highlight%28y=8%29
6x-7=53-->6x=53%2B7-->6x=60-->x=60%2F6-->highlight%28x=10%29

You are not telling me what/where point E is,
but I am guessing that it is the intersection of the diagonals of the rhombus.
Since B and D are opposite vertices, BD is a diagonal,
and if E is the intersection of both diagonals,
then E is the midpoint of both diagonals and ED=BE .
That gives us the equation
5z-7=3z-1-->5z-3z=7-1-->2z=6-->z=6%2F3-->highlight%28z=3%29 .
That makes
ED=5%2A3-7=15-7=8 and BE=3%2A3-1=9-1=8 , which verifies.

Most importantly, with BE=8 and EC=6
are the legs of right triangle BEC, so
the Pythagorean theorem says that the length of the hypotenuse is
BC=sqrt%288%5E2%2B6%5E2%29=sqrt%2864%2B36%29=sqrt%28100%29=10 .
That makes the length of each side of ABCD 10 (in whatever units),
and the perimeter of ABCD is 4%2A10=highlight%2840%29 .

NOTE:
The teacher proposing this problem used a 2X scaled up version of the very popular right triangle with side lengths 3, 4, and 5 to design the rhombus.
That would make tan%28BAC%29=8%2F6=4%2F3=1.333%28rounded%29 .
However, the solution to the problem involves BAC=53%5Eo ,
and tan%2853%5Eo%29=1.327%28rounded%29 , which is not quite equal,
but very close to 4%2F3=1.333%28rounded%29 .
Using the fact that sin%2853%5Eo%29=0.7986%28rounded%29 ,
you would not have needed the length of EC,
and could have calculated BC=approximately8%2F0.7986=10.02 .
That tells me that you were obviously not expected to use trigonometric functions, but the problem designer tried to make it believable by choosing 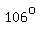106%5Eo for angle BCD.