Question 1154920: The diagonals of quadrilateral ABCD intersect at E(- 1, 4) . ABCD has vertices at A(1, 7) and B(- 4.5) What must be the coordinates of C and D to ensure that ABCD is a parallelogram?
Found 3 solutions by jim_thompson5910, MathLover1, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Start at point A(1,7). To move to point E(-1,4), we need to move 3 units down and 2 units to the left. We can see this in the diagram below.

Repeat this pattern of "down 3, left 2" one more time and you'll arrive at point C(-3,1)

----------------------------
Now focus on point B(-4, 5). To move from here to E(-1,4), we move 1 unit down and 3 units to the right. Do this again to arrive at point D (2,3)

These moves are valid because AE = EC, and BE = ED. Recall that the diagonals of any parallelogram always bisect each other. "Bisect" means to "cut in half".
You can go without using a visual diagram. Instead, you can use coordinate geometry. To go from A to E, we subtract 2 from the x coordinate and subtract 3 from the y coordinate. We can say the translation rule is  \to (x-2,y-3)) . If you apply this translation rule to point E, then E moves to point C's location. Similarly, the translation rule of . If you apply this translation rule to point E, then E moves to point C's location. Similarly, the translation rule of  \to (x+3,y-1)) is used to go from B to E. Use it on point E to move it to point D. is used to go from B to E. Use it on point E to move it to point D.
Final Diagram

To prove that we have a parallelogram, all you need to do is show that the opposite sides are parallel. To do this, compute the slopes of segments AB and CD. You should find the slopes to be equal. Parallel lines always have equal slopes. You should also find that segments BC and AD have equal slopes as well, so they are parallel also.
Answers:
C is at (-3, 1)
D is at (2, 3)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The diagonals of quadrilateral 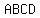 intersect at E( intersect at E(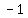 , , ) . ) .
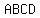 has vertices at A( has vertices at A( , ,  ) and B( ) and B(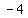 , , ) )
What must be the coordinates of  and and  to ensure that to ensure that  is a parallelogram? is a parallelogram?
The diagonals of a parallelogram bisect each other. So, the distance from  to to  is same as the distance from is same as the distance from  to to  , and the distance from , and the distance from  to to  is same as the distance from is same as the distance from  to to 
=> E( , , ) is mid-point ) is mid-point
then, use mid-point theorem to find coordinates ( , , ) of ) of  and and 
E( , , ) is mid-point of A( ) is mid-point of A( , ,  ) and ) and  = = , , ) )






=> = = , , ) )
E(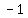 , , ) is mid-point of B( ) is mid-point of B(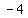 , , ) and ) and  = = , , ) )






=> = = , , ) )
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by @MathLover1 is W R O N G.
You can not use it. Do not use it. For your safety, ignore it.
Use the solution by Jim, instead.
--------------
@Mathlover  assumes that the point E is the middle of AD, but it is not so. assumes that the point E is the middle of AD, but it is not so.
Next, she  assumes that the point E is the middle of BC, but it is not so, too. assumes that the point E is the middle of BC, but it is not so, too.
Wrong assumptions lead her to wrong solution and to wrong answer.
/\/\/\/\/\/\/\/
Dear tutor @MathLover1,
don't you think that it is just time for you to take a break at this forum ?
|
|
|