The lesson title
In a parallelogram, each diagonal
divides it in two congruent triangles
Properties of the sides of a parallelogram
Properties of the sides of parallelograms
Properties of diagonals of parallelograms
Opposite angles of a parallelogram
Consecutive angles of a parallelogram
The lesson title
Midpoints of a quadrilateral are vertices
of the parallelogram
The length of diagonals of a parallelogram
Remarcable advanced problems on parallelograms
|
The property
In a parallelogram, each diagonal divides it
in two congruent triangles.
In a parallelogram, the opposite sides are of equal
length in pairs.
If in a quadrilateral the opposite sides are of equal
length in pairs, then the quadrilateral is a parallelogram.
If a quadrilateral has two opposite sides parallel
and of equal length, then two other opposite sides
are parallel and of equal length too.
If in a quadrilateral two opposite sides are parallel
and two other opposite sides are parallel too, then
the opposite sides of each pair are of equal length.
In a parallelogram, the two diagonals bisect each other.
If in a quadrilateral the two diagonals bisect each other,
then the quadrilateral is a parallelogram.
In a parallelogram, the opposite angles are congruent.
If in a convex quadrilateral the opposite angles are
congruent, then the quadrilateral is a parallelogram.
In a parallelogram, the sum of any two consecutive
angles is equal to 180°.
If in a quadrilateral the sum of any two consecutive
angles is equal to 180°, then the quadrilateral is
a parallelogram.
The property
In a convex quadrilateral the midpoints of its sides
are vertices of the parallelogram.
If a, b, c and d are the lengths of the sides of a parallelogram
and  and and  are the lengths of its diagonals, then are the lengths of its diagonals, then
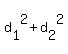 = = 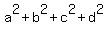 = =  . .
In a parallelogram the segments connecting the opposite
vertices with the midpoints of the parallel sides cut
the diagonal in three congruent parts.
In a parallelogram the lengths of the adjacent sides are
8 cm and 3 cm respectively. Angle bisectors drawn from the vertices
of the long side split the opposite side into three segments.
Find the length of each of these segments.
|
Under the topic
Parallelograms
Parallelograms
Triangles
Parallelograms
Parallelograms
Parallelograms
Under the topic
Geometry
Geometry
Parallelograms
|
In the section
Geometry
Geometry
Geometry
Geometry
Geometry
Geometry
In the section
Word problems
Word problems
Geometry
|

