Question 970825: For what value(s) of m is the line y = mx + b at a distance 3 from (4,1) ??
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe you have an infinite number of values of m that would satisfy this.
all points at a distance of 3 from (4,1) form a circle with (4,1) at the center.
all radii of that circle would be straight lines that are a distance of 3 from the center of that circle.
there are an infinite number of points where this can occur.
this leads to an infinite number of lines connecting from those points to the center of the circle.
this leads to an infinite number of slopes, one for each of those infinite number of lines.
i believe the answer would be the set of all (x,y) where y = plus or minus sqrt(9-(x-4)^2)+1
that equation comes from the equation of a circle with radius of 3 and center at (4,1), that equation being (x-4)^2 + (y-1)^2 = 9
the graph of that equation would look like this:

the center of that circle is at (4,1).
the distance from any point on the circle to the center of that circle is equal to 3.
for example, we'll pick a value of x at random, where x is less than or eqjual to to 3 units from x = 4.
let's try x = 5
when x = 5, one of the y's would be equal to sqrt(9-(x-4)^2)+1 which would be equal to sqrt(9-(5-4)^2)+1 which would be equal to sqrt(8)+1.
the point (5,sqrt(8)+1) that lies on the circle should be 3 units away from the point (4,1).
the length of the line between (4,1) and (5,sqrt(8)+1) is given by sqrt((x2-x1)^2 + (y2-y1)^2) which is equal to sqrt((5-1)^2 + (sqrt(8)+1-1)^2) which is equal to sqrt(1^2 + sqrt(8)^2) which is equal to sqrt(9) which is equal to 3 which is the correct distance.
the slope of that line is (y2-y1) / (x2-x1) = (sqrt(8)+1 - 1) / (5-4) = sqrt(8)/1 = sqrt(8).
the equation of that line is y = sqrt(8)*x - 4*sqrt(8) + 1.
here's a graph of the equation of that line and the circle.
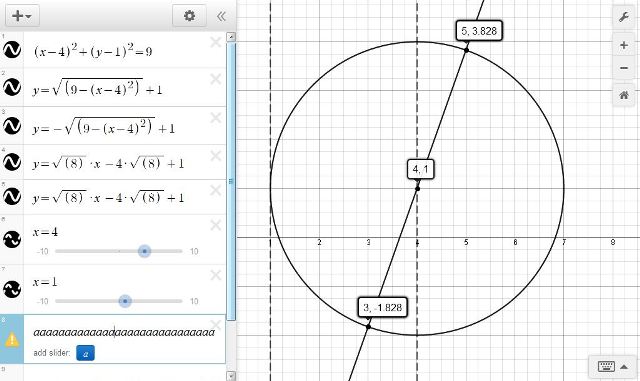
as you can see, the line goes through the center of the circle which forms two radii, one from (4,1) to (5,3.828) and from (4,1) to (3,-1.828).
the easy way to calculat the radius is to look at the horizontal line from (4,1) to (7,1) where it's eqasy to see that the distance between the center of the circle and a point on the circle is equal to 3.
all radii of the circle are the same distance from the center of the circle.
an infinite number of lines can be formed with an infinite number of slopes, one for each of those lines.
that's my impression.
|
|
|