Question 782850: 

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  <--> <-->  <--> <-->  <--> <-->  <--> <-->  <--> <-->  <--> <-->  <--> <--> 
To solve an equation like  , we tranform it into simpler and simpler equivalent equations in several steps. , we tranform it into simpler and simpler equivalent equations in several steps.
(Equations are called equivalent when they have exactly the same solutions).
An equation can be transformed into an equivalent equation by:
adding the same number (or expression) to both sides of the equal sign, or
subtracting the same number (or expression) from both sides of the equal sign, or
multiplying times the same non-zero number (or expression) both sides of the equal sign, or
dividinging by the same non-zero number (or expression) both sides of the equal sign.
The steps used above were:
subtract  from both sides, from both sides,
subtract 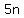 from both sides, and from both sides, and
divide both sides by  . .
Why those steps in that order?
Because we have to "undo" all the bad tricks played on  until we get to an equation looking like until we get to an equation looking like  . .
Such an equation is the solution.
The rules about order of operations were established long ago so that we could all agree on what we meant when we talk math in "full sentences".
According to the rules of order of operations, in the expression  , ,  was "dressed up" by first multiplying times was "dressed up" by first multiplying times  , and then adding , and then adding  . .
We need to "undress" it.
To do that, we start by undoing the last "dressing" step first.
So we undo the adding  by subtracting by subtracting  . .
After that the left side is simpler, just  , but we have , but we have  on both sides. on both sides.
By subtracting 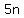 from both sides, we can get a simpler right side (just from both sides, we can get a simpler right side (just  ), and end up with ), and end up with  appearing only on the left side. appearing only on the left side.
That leaves us with  , where , where  is multiplied times is multiplied times  . .
We "undo that multiplication by dividing by  . .
NOTE 1:
 <--> <--> 
shows two equivalent equations, but does not help in solving the first equation.
NOTE 2:
The equation  is not equivalent, because the is not equivalent, because the 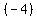 is not multiplied times the entire left side, and times entire right side of the equation. is not multiplied times the entire left side, and times entire right side of the equation.
It is multiplying only  on the left, and only on the left, and only  on the right. on the right.
|
|
|