Question 775450: 20 1/2, 23 1/3, 26 1/6, 29... what would the 7 term be in this sequence and how would you find it?
Found 2 solutions by Edwin McCravy, MathLover1:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website! 20 1/2, 23 1/3, 26 1/6, 29...
Subtract 2nd term minus 1st term
23 1/3 = 23 2/6 = 22 8/6
-20 1/2 = -20 3/6 = -20 3/6
---------------------------
2 5/6
Subtract 3rd term minus 2nd term
26 1/6 = 26 1/6 = 25 7/6
-23 1/3 = -23 2/6 = -23 2/6
---------------------------
2 5/6
Subtract 4th term minus 3rd term
29 28 6/6
-26 1/6 = -26 1/6
-----------------
2 5/6
So the common difference is 2 5/6
So we add 2 5/6 each time to get the next term:
29
+ 2 5/6
-------
31 5/6 = 5th term
31 5/6
+ 2 5/6
-------
33 10/6 = 34 4/6 = 34 2/3 = 6th term
34 2/3 = 34 4/6
+ 2 5/6 + 2 5/6
-----------------
36 9/6 = 36 3/2 = 37 1/2 = 7th term.
Edwin
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website! given:
20 1/2, 23 1/3, 26 1/6, 29.
or you can write them this way:
41/2, 70/3, 157/6, 29, ..........
To find any term of an arithmetic sequence:
 where 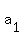 is the first term of the sequence,  is the common difference,  is the number of the term to find.
here is more terms of your sequence:
41/2, 70/3, 157/6, 29, 191/6, 104/3, 75/2, 121/3, 259/6, 46, 293/6, 155/3, 109/2, 172/3, ...
|
|
|
