Question 758451: Could you please help me solve this problem:-
There are fewer than 30 students in a math's class and this year the grades are given out as follows -
one third of the students got an A
one quarter of the students got a B
four students got a C and
three students got an E
How many students got a D?
My understanding is that there must be 29 or less students in the class to begin with. My next step I think I have to do is work out what fraction is 1/3 + 1/4 + the 4 + 5 students which got a grade away from this number of 29 or less and this will give me the answer.
Now I know the answer is 5 (the sheet tells me) but I am lost in how you work out this equation. Could you please show me how to calculate this formula - I am a mature student trying to re-visit long ago maths and am finding many missing parts lol.
Many thanks & most appreciated
Angie
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this is what i see from this problem.
your basic equation is x/3 + x/4 + 4 + D + 3 < 10
this can be simplified to:
x/3 + x/4 + 7 + D < 30
since x has to be an integer, than x has to be divisible by 3 and also by 4.
this means that x has to be a multiple of both 3 and 4 and has to be smaller than 30.
multiples of 3 less than 30 are:
3,6,9,12,15,18,21,24,27
multiples of 4 less than 30 are:
4,8,12,16,20,24,28
the least common multiple is 12.
the next least common multiple is 24.
those are the only 2 numbers < 30 that are integers that can represent the total number of students that can possibly satisfy the equation.
when x = 12, you get the following:
A = 12/3 = 4
B = 12/4 = 3
C = 4
D = D
E = 3
The total of students becomes 14 + D which is greater than 12, so the total number of students can't be 12.
when x = 24, you get the following:
A = 24/3 = 8
B = 24/4 = 6
C = 4
D = D
E = 3
the total of students becomes 21 + D
since the total of student is equal to 24, D must be equal to 3.
D = 3 is your solution.
i don't know how 5 can be a solution and you can wind up with integer values for everything.
when D = 5, you get:
A = x/3
B = x/4
C = 4
D = 5
E = 3
the total of students is equal to x/3 + x/4 + 12 which must be less than 30.
this means that x/3 + x/4 must be less than 18.
once again, x must be an integer and the only common multiple less than 18 is equal to 12 and it was already shown up above that x can't be equal to 12.
the key to solving this problem is that x has to be an integer.
without taking that into consideration, you run into difficulty as i did when i didn't make that assumption.
this is because the equation is equal to less than 30 which makes 29 possible values of x that have to be solved for independently and, when you do that, you will find that most of them wind up with the value of x or the value of D not being an integer.
the possible solutions for every value of x < 30 where x is an integer are shown in the following table:
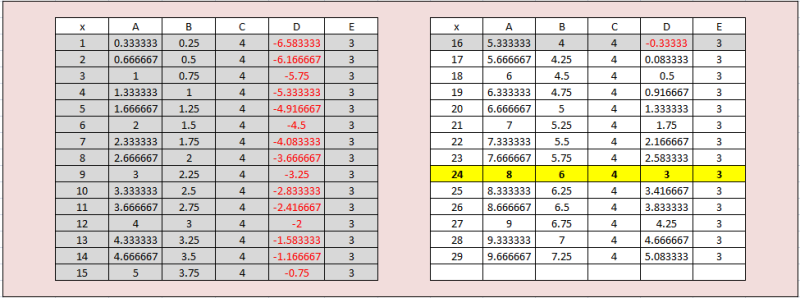
from the table, you can see that D is negative when x is smaller than or equal to 16.
from the table, when x is greater than 16 and less than 30, you can also see that A, B, and D are integers only when x is equal to 24.
|
|
|