Question 479514: if a,b,c and d are in set of natural numbers(N) with a=bcd, b=cda and d=abc then,what is the value of (a+b+c+d)^2 ?
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since  and and  , we can substitute b into the first equation and obtain , we can substitute b into the first equation and obtain  , which can be simplified into , which can be simplified into  . Since a,b,c,d are natural numbers (not equal to zero), we can divide both sides of the last equation by a and obtain . Since a,b,c,d are natural numbers (not equal to zero), we can divide both sides of the last equation by a and obtain  . Again, using the fact that a,b,c,d are natural numbers we conclude that both c and d are equal to 1. . Again, using the fact that a,b,c,d are natural numbers we conclude that both c and d are equal to 1.
Now we have to find values of a and b. We can use the last equation  and substitute c = 1 and d = 1 to obtain and substitute c = 1 and d = 1 to obtain  . Again, a and b are natural numbers, and thus both equal to 1. So, the only solution to the system of equations for a,b,c,d among the set of natural numbers is all of the being equal to 1. . Again, a and b are natural numbers, and thus both equal to 1. So, the only solution to the system of equations for a,b,c,d among the set of natural numbers is all of the being equal to 1.
Thus 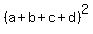 is equal to 16. is equal to 16.
|
|
|