Question 346670: Please help me with this Math question:
sqrt150 - sqrt24 -sqrt54
Sorry I don't remember how to do the sign for square root on the computer.
Thank you!!!
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't think you are supposed to use a computer or calculator, even if you remember how to use them to find square roots. All computers or calculators can do with most square roots is to find a decimal approximation for the square root.
Instead, I believe your problem is to simplify the expression. Simplifying square roots involves finding perfect square factors of the radicand, if any. ("Radicand" is the name for the expression inside a radical (like a square root).) So we will start by looking for perfect square factors in each of the radicands and, if we find them, rewriting the radicands as a product involving these perfect squares:
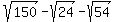
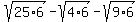
Next we use a property of radicals,  , to separate the perfect squares factors into their own square roots: , to separate the perfect squares factors into their own square roots:
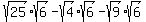
Now we can replace the square roots of the perfect squares:
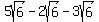
Now the square roots have been simplified. Next we simplify the expression as a whole, if possible. It turns out that these are like terms so they can be added/subtracted. (If you have trouble seeing this, perhaps using a temporary variable will help. Let  . Then the expression becomes: . Then the expression becomes: 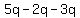 . This, I hope you can see, is an expression of like terms. And so is the expression with the square roots of 6!) . This, I hope you can see, is an expression of like terms. And so is the expression with the square roots of 6!)
As it turns out, subtracting 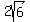 from from  leaves leaves 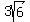 (just like 5q - 2q = 3q). And if we then subtract (just like 5q - 2q = 3q). And if we then subtract 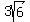 from from 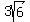 we get 0. we get 0.
So the simplified expression is zero!
|
|
|