Question 281528: What are ways for factoring in an organized way?
Answer by Mathematicians(84)   (Show Source):
You can put this solution on YOUR website! Starting from easiest to most complicated:
Greatest common factoring:
Take out the greatest common factor:
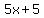
Since 5 is in both:
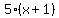
Trinomial factoring (easy):
This example will have nothing near the x^2
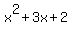
You need to find two things that add up to 3 and multiply to be 2.
In this case, 1 and 2 are your answers because 1 + 2 = 3 and 1 * 2 = 2
so 
Factor by grouping:
This will not work all the time.
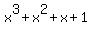
Group the first two terms and the last two terms:
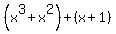
We can use greatest common factoring, x^2 is the same in the first two terms and 1 is the same in the next two.
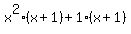
At this step, you can tell if grouping will work, you will see that we have two (x+1), from this step, you can factor out an (x+1) from each term:
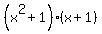 many people see this step as taking only one of the (x+1) terms and taking the x^2, and the +1 and put it together.
Trinomial factoring (hard):
This example will have something near the x^2
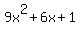
The method to do this one is to multiply the first and last number together:
Now you want to do something similar to the first one, two things that multiply to be 9 and add up to be 6. The answer is 3 and 3, so we divide the middle up like this:
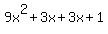
If all went right, you can factor by grouping:
Those should be all the factoring methods you will need to know, the other one is much tougher but is very tricky and is taught at higher levels.
|
|
|
