Question 222436: Number: 192 Factors Are: (96,2)(64,3)(48,4)(32,6)(24,8)(16,12)
Number: 256 Factors Are: (128,2)(64,4)(32,8)
(256×a×b×c×d)/(192×b×c×d)=(2×2×2×2×2×2×2×2×a×b×c×d)/(2×2×2×2×2×2×3×b×c×d)=4abcd/3bcd= 1 1a/3
Do I cancel the letters or should the amnswer be, 1 1abcd/3bcd
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! Yes! The "letters" all cancel out, and all you are left with is the fraction 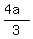 . You can also write this as 1 1/3 a, but the improper fraction 4a/3 is usually preferred. By the way, you went to a lot of trouble to find all the factor combinations of 192 and 256. I think it's easier to break down a number using what is called a "factor tree." I can't really show this in the algebra.com format, but you can see what I mean on my own website.
Do a "Bing" search for my last name "Rapalje". Look for "Rapalje Homepage" near the top of the search list. On my Homepage near the top, look for the link "Basic, Intermediate and College Algebra: One Step at a Time." Choose "Basic Algebra", and look in Chapter 2, Section 2.02 "FACTORING NUMBERS." In this section, you will find my own non-traditional explanations, that my own students all said were a LOT easier to understand than traditional textbooks.
R^2
Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Altamonte Springs Campus
|
|
|
