Question 134264: If 15 points are arranged on a circle, how many lines are needed to join every point to every other point once?
Please help me!!
- Jordan
Found 2 solutions by scott8148, josmiceli:
Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website! 15 points, each joined to 14 other points is 15*14 or 210
BUT, point A to point B is the SAME line as point B to point A; so half the lines are duplicates
210*(1/2)=105
Answer by josmiceli(19441)  (Show Source):
You can put this solution on YOUR website! One way to start thinking about it is to play around with a fewer number of
points, say 5 equally spaced around a circle. Label the points 1-5
Starting at point 1, draw lines to the other 4 points. You have 4 lines,
or (5 - 1).
From point 2, draw lines to the other 4 points. You have 4 lines, but the
line to point 1 was already there, so subtract 1.
So far you have
from point 1: (5 - 1)
from point 2: (5 - 1) - 1
From point 3 draw lines to the other 4 points. You have 4 lines, but the
lines to point 1 and point 2 were already there, so subtract 2
Now finish for all 5 points
from point 1: (5 - 1)
from point 2: (5 - 1) - 1
from point 3: (5 - 1) - 2
from point 4: (5 - 1) - 3
from point 5: (5 - 1) - 4
Doing the additions and subtractions , I get
 lines. I counted them- it works
Now I can come up with a formula for any number of points
arranged on a circle and use it for 15 points
Let  = the number of points
Let  = the number of different lines connecting the points
 - (the sum 1 + 2 + 3 + 4 + . . . + (n - 1))
There is a formula for the sum. It is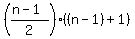 
which simplifies to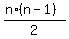 
So far, the formula is
 general formula
Now see if this formula works for 5 points
 It works
Now for 15 points
 answer
Hope this didn't confuse you
The general formula should work for any number of points
|
|
|
