Question 1209939: If m is a positive integer and sqrt(4m^2+29) is an integer, then what is m?
Found 4 solutions by math_tutor2020, ikleyn, mccravyedwin, AnlytcPhil:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: m = 7
Work Shown
k = some integer
k = sqrt(4m^2+29)
k^2 = 4m^2+29
k^2-4m^2 = 29
(k-2m)(k+2m) = 29
29 is prime so the only factors are 1 and 29.
k and m are integers, so k-2m and k+2m are also integers.
In order for (k-2m)(k+2m) = 29 to be the case, we'd need either

or

In either system of equations, adding straight down leads to 2k = 30 which solves to k = 15.
Then,
k-2m = 1
15-2m = 1
-2m = 1-15
-2m = -14
m = -14/(-2)
m = 7
Or,
k-2m = 29
15-2m = 29
-2m = 29-15
-2m = 14
m = 14/(-2)
m = -7
We ignore m = -7 since your teacher stated that m > 0
Check: sqrt(4m^2+29)=sqrt(4*7^2+29)=15 is an integer.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If m is a positive integer and sqrt(4m^2+29) is an integer, then what is m?
~~~~~~~~~~~~~~~~~~~~~~~~~
If 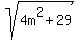 is an integer number n, then
4m^2 + 29 = n^2
29 = n^2 - 4m^2
29 = (n-2m)*(n+2m).
29 is a prime number, so it has two possible decompositions into the product of prime factors
29 = 1* 29 or 29 = (-1)*(-29).
Therefore, we have 4 systems of linear equations to analyze
n - 2m = 1, (1)
n + 2m = 29, (2)
n - 2m = -1, (3)
n + 2m = -29, (4)
n - 2m = 29, (5)
n + 2m = 1, (6)
n - 2m = -29, (7)
n + 2m = -1. (8)
From system (1), (2), by subtracting equations, we have
2m - (-2m) = 29-1, 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), and it works properly: is an integer number n, then
4m^2 + 29 = n^2
29 = n^2 - 4m^2
29 = (n-2m)*(n+2m).
29 is a prime number, so it has two possible decompositions into the product of prime factors
29 = 1* 29 or 29 = (-1)*(-29).
Therefore, we have 4 systems of linear equations to analyze
n - 2m = 1, (1)
n + 2m = 29, (2)
n - 2m = -1, (3)
n + 2m = -29, (4)
n - 2m = 29, (5)
n + 2m = 1, (6)
n - 2m = -29, (7)
n + 2m = -1. (8)
From system (1), (2), by subtracting equations, we have
2m - (-2m) = 29-1, 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), and it works properly:
 = = 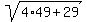 = = 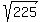 = 15.
From system (3), (4), by subtracting equations, we have
2m - (-2m) = -29-(-1), 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (5), (6), by subtracting equations, we have
2m - (-2m) = 1-29, 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (7), (8), by subtracting equations, we have
2m - (-2m) = -1 - (-29), 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), the same as we got from system (1), (2),
and it works properly: = 15.
From system (3), (4), by subtracting equations, we have
2m - (-2m) = -29-(-1), 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (5), (6), by subtracting equations, we have
2m - (-2m) = 1-29, 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (7), (8), by subtracting equations, we have
2m - (-2m) = -1 - (-29), 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), the same as we got from system (1), (2),
and it works properly:  = = 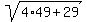 = = 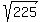 = 15.
ANSWER. For the given problem, there is a unique solution for m. It is m = 7. = 15.
ANSWER. For the given problem, there is a unique solution for m. It is m = 7.
Solved.
I placed this my solution here after the solution by tutor @math_tutor2020 to make the analysis complete.
///////////////////////////
My comment/response to the Edwin's comment, regarding my post.
For this given problem, considering all four decompositions
29 = 1*29 = 29*1 = (-1)*(-29) = (-29)*(-1)
is NECESSARY for the completeness of the analysis.
So, all 4 (four) cases/decompositions MUST be considered, exactly as it was made in my post.
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Ikleyn states
29 is a prime number, so it has two possible decompositions in the product of
prime numbers
29 = 1* 29 or 29 = (-1)*(-29).
But unless we are in modern algebra where there are such things as "groups",
"rings", etc., and where "prime number" has a different definition, then "prime
number" always means a positive integer with exactly 2 unique positive integer
factors.
While 29 = (-1)*(-29) is true, it is not a decomposition in the product of prime
numbers.
Edwin
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Ikleyn states
29 is a prime number, so it has two possible decompositions in the product of
prime numbers
29 = 1* 29 or 29 = (-1)*(-29).
You may not say that. You may say:
29 is a prime number, so it has ONE possible decomposition in the product of
prime numbers
29 = 1* 29.
Or you may say:
29 is a prime number, so it has two possible decompositions in the product of
integers.
29 = 1* 29 or 29 = (-1)*(-29).
Edwin
|
|
|