Question 1209284: which of the following numbers is the smallest? A. 3/7 B.1/3 C.5/6 D.9/14
Found 3 solutions by ikleyn, mccravyedwin, math_tutor2020:
Answer by ikleyn(52933)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
which of the following numbers is the smallest? A. 3/7 B.1/3 C.5/6 D.9/14
~~~~~~~~~~~~~~~~~~~~~~~~~~
Write these numbers with the common denominator.
The Least Common Denominator (LCD) is 7*3*2 = 42.
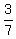 = = 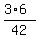 = = 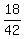 . .
 = = 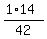 = = 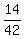 . .
 = = 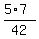 = = 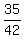 . .
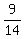 = = 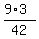 = = 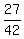 .
Comparing fractions (their numerators), you see that .
Comparing fractions (their numerators), you see that 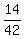 is the smallest number.
ANSWER. is the smallest number.
ANSWER. 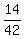 = =  is the smallest number. is the smallest number.
Solved.
---------------------
There are other, even more effective ways to find the smallest number.
For example, 1/3 multiplied by 3 gives 1.
All other listed numbers, multiplied by 3, give the product greater than 1 (which is OBVIOUS).
It means that 1/3 is the smallest number among the listed.
Nevertheless, the explanation, which I gave in first part of my post, is the #1 explanation
to this question, which a teacher usually provides to students in the class at normal study process.
All other explanations are #2, #3, #4 and so on . . .
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An alternate way, if you are allowed to use a calculator,
such as when you're at home, and want to check your answer to
see if they're correct.
Just get a calculator, divide them out and line up the decimal points:
A. 3/7 = 3÷7 = 0.4285714286...
B. 1/3 = 1÷3 = 0.3333333333...
C. 5/6 = 5÷6 = 0.8333333333...
D. 9/14 = 9÷14 = 0.6428571429...
Look at the column of first digits. They're all the same, 0, so you can't tell.
Look at the 2nd digits, (the first ones after the decimal). They are 4,3,8,6.
That's all you need. 3 is the smallest, so 1/3 is the smallest.
If the column of first digits are all the same, you go to the column of second
digits and pick the smallest. If the second digits are all the same, you go to
the column of third digits and pick the smallest, etc., etc.
----------------------------------------------------------------------
Suppose you were given this problem to find the smallest:
A. 37/140 B. 183/700 C. 46/175 D. 939/3500
A. 37/140 = 37÷140 = 0.2642857143...
B. 183/700 = 183÷700 = 0.2614286714...
C. 46/175 = 46÷175 = 0.2628571429...
D. 939/3500 = 939÷3500 = 0.2682857143...
You would have to go to the column of 4th digits (3rd digits after the decimal),
4,1,2,8 to see that the smallest would be 183/700.
Edwin
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website! Answer: 1/3
Explanation
The other tutors have great responses.
I'll offer another approach.
Let's compare the fractions A and B
For now assume they are equal.
We can use the cross multiplication rule like so
3/7 = 1/3
3*3 = 7*1
9 = 7
The last equation is false since the two sides don't agree on the same number.
To fix the error, change each equal sign to a greater than sign.
3/7 > 1/3
3*3 > 7*1
9 > 7
We determine that 3/7 is larger than 1/3.
Cross choice A off the list.
So far 1/3 is the smallest value.
But there could be another fraction in this list that's smaller.
Now let's compare B and C.
Like before we assume they are equal, and use the cross multiplication rule to get,
1/3 = 5/6
1*6 = 3*5
6 = 15
This is false, so let's fix the errors.
1/3 < 5/6
1*6 < 3*5
6 < 15
The fraction 1/3 is still the smallest so far.
Cross choice C off the list.
The last comparison is to look at B and D.
1/3 = 9/14
1*14 = 3*9
14 = 27
Let's fix the errors
1/3 < 9/14
1*14 < 3*9
14 < 27
Cross choice D off the list since D is larger than B.
Therefore 1/3 is the smallest fraction in the list.
|
|
|